投稿日: 投稿者: yasufumi.yamada1@gmail.com

計算数理A演習第10回

コンテンツ

第１０回

１次元拡散方程式の数値解法

これまでは変数が時間にのみ依存するものを扱っていましたが、今回からは、時間以外に空間にも依存する変数を扱います。つまり、変数としてはu(x,t)と書けます。１次元拡散方程式（１次元熱伝導方程式とも呼ばれる）の初期値境界値問題を数値的に解きます。
それは、次のようなものです。（教科書や文献によって記号など多少異なるかもしれません。）

問題１.１

\displaystyle \frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} ~~ (0 < x < L, t> 0),
u(0, t) = 0,
u(L, t) = 0~~(t>0),
u(x, 0) = 2x(L-x)~~(0\le x \le L)

1行目の式は拡散方程式、もしくは熱伝導方程式と呼ばれます。式中のDは拡散係数または熱伝導率とよばれます。
拡散とは物が散らばっていく様子（例：コップにインクを垂らすと、時間とともに広がって最後には一様になる）であり、熱伝導とは熱が伝わる様子（例：スプーンを熱湯に浸けていると徐々に熱が伝わって持っている部分まで熱くなる）です。
これらの現象を表現しているのが上式なのです。
「物の散らばり」と「熱の伝わり」という異なる現象が同じ方程式で表されるというところは、数式の面白さといって良いでしょう。
熱伝導方程式と見るとu(x,t)は時刻tでの温度分布、拡散方程式とするとu(x,t)は粒子の密度分布に対応し、何れにしても、分布が時間的な変化を考えることができます。

2行目と3行目の式は境界条件と呼ばれ、空間の端の部分（x=0およびx=L）での拘束条件になります。
問題1では、x = 0とx = Lでいつもu = 0となるディリクレ境界条件を境界に課しています。
温度の分布の言葉でいうと、両端を氷か何かでつねに冷やしている状況を考えていることになります。
つまり、熱が両端からどんどんと奪われているわけです。

4行目の式は、初期条件（t=0）です。

以下では、拡散方程式・熱伝導方程式という呼称を拡散方程式に統一します。

空間と時間の分割

さて、計算機で扱えるよう離散化し、数値的に近似解を求めます。
これまでの常微分方程式の解法では、数値計算において、時間という本来連続な変数をそのまま扱うわけにはいかないため、t=t_i~(i=0,1,\cdots,N)のように離散化をしていたわけですが、もう一つ増えた空間を表す変数xについても同様に離散化をする必要があります。ただし、以下のように、空間方向の分割方法は時間方向の分割方法とは少し異なります。

上図の(1)は時間方向の分割方法で、これまでと変わりません。数直線で書き表すと、考える範囲をI等分した目盛り上に位置します。一方、空間方向の分割は、考える範囲をI等分するところまでは同じようにしますが、そこから目盛と目盛の中間の点に空間座標がきます。なぜこのような面倒なことをするのか、というと、境界条件について考えやすいためです（後述）。

空間の区切り方のイメージとしては、アパートのように同じ間取りの部屋で区切り、隣との壁が目盛り、物質の濃度や温度は部屋の中心で測る、といった感じでしょうか。アパートでは隣の部屋の物質が壁を通過して流れ込んだりすることはそうそうないですが、断熱材が少ないアパートは熱は多少なりとも伝わっていったりします。両隣の部屋がエアコンをガンガンにつけていると、真ん中の部屋の光熱費は少なくて済むかも？

これまでhを時間刻み幅としてきましたが、今後はhを空間刻み幅、\tauを時間刻み幅とします。すなわち、空間方向では[0, L]区間をN等分（h=L/N）、時間方向では[0, T]区間をM等分（\tau=T/M）して、x_j = (j - 1/2)h, t_k = k\tauおくことができ、

\[ U^k_j \approx u(x_j, t_k), \ \ (j=1, \cdots, N, k= 0, 1, \cdots , M)\]

と書くことができます。

差分方程式

上記の拡散方程式と境界条件・初期条件を以下のように差分化します。

拡散方程式の差分化

拡散方程式は、上記の差分化を使えば、

$$\frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} $$

\[ \frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} \]

は次の差分方程式で近似されます。

$$ \frac{1}{\tau} (U_j^{k+1} – U_j^k) = D\frac{\frac{U_{j+1}^k – U_j^k}{h} – \frac{U_j^k – U_{j-1}^k}{h}}{h}, \ \ (j=1, \cdots, N, k= 0, 1, \cdots ,M)$$

これを整理すると、

$$ \frac{1}{\tau} (U_j^{k+1} – U_j^k) = \frac{D}{h^2}(U_{j-1}^k – 2U_j^k + U_{j+1}^k), \ \ (j=1, \cdots, N, k= 0, 1, \cdots ,M)$$

になります．さらに，これを書き換えれば，

$$U_j^{k+1} = \alpha U_{j-1}^k + (1 – 2\alpha) U_j^k + \alpha U_{j+1}^k, \ \ (j=1, \cdots, N, k= 0, 1, \cdots ,M)$$

が得られます。ただし、\alpha = D\tau / h^2としました。
この式は見てのとおり、時刻t_kでのuから次の時刻t_{k+1}でのuの値が計算できる形をしています。

境界条件の差分化

今回は境界条件はディリクレ境界条件ですが、他にもよく使う境界条件であるノイマン境界条件・周期境界条件も導出しておきましょう。

ディリクレ境界条件

ディリクレ境界条件の一般的な形式は次の通りです。

\[u(0, t) = c,u(L, t) = c~(t>0)\]

x=0について考えると、x=0の目盛り上で時間に依らず常にある一定値c（今回はc=0）となるためには、境界の両隣の2点の中間値がcになれば良いので、

\[\displaystyle \frac{U_0^k+U_1^k}{2} = c\]

より、

\[U_0^k=2c-U_1^k~ (k=0, 1, 2, \cdots ,M)\]

とすれば良いです。反対側のx=Lの境界も同様に

\[U_{N+1}^k = 2c-U_N^k~ (k=0, 1, 2, \cdots ,M) \]

となります。

ノイマン境界条件

ノイマン境界条件は以下の通りです。

\[\frac{\partial u(0, t)}{\partial x} = 0, \frac{\partial u(L, t)}{\partial x} = 0~~(t>0)\]

x=0について考えると、x=0の目盛り上で時間に依らず常に空間方向の微分が0とならなければならないのですが、空間方向は離散的に区切られています。そこで、

\[\frac{\partial u(0, t)}{\partial x}\approx\frac{U_1^k-U_0^k}{h} = 0\]

より、

\[U_0^k=U_1^k~ (k=0, 1, 2, \cdots ,M)\]

とすれば良いです。反対側のx=Lの境界も同様に

\[U_{N+1}^k = U_N^k~ (k=0, 1, 2, \cdots ,M) \]

となります。

周期境界条件

周期境界条件は、周期的になっていれば良いのですが、周期関数の定義

\[u(x)=u(x+L)\]

を使って考えます。境界を超えて、x<0やx>L” height=”12″ width=”46″>も同じように関数が繰り返されると考えれば良いので、</p> <figure class=U_0^k=U_N^k

U_{N+1}^k=U_1^k

となります。

初期条件

初期条件は、xの離散化のみ考えればよく、

$$U_j^0 = 2x_j(L-x_j) ~(j=1, 2, \cdots ,N)$$

になります。

これで、準備はできました。

次に拡散方程式を計算機にて解くためのアルゴリズムを考えましょう。

計算ルーティンについては以下のイラストを参照してください．


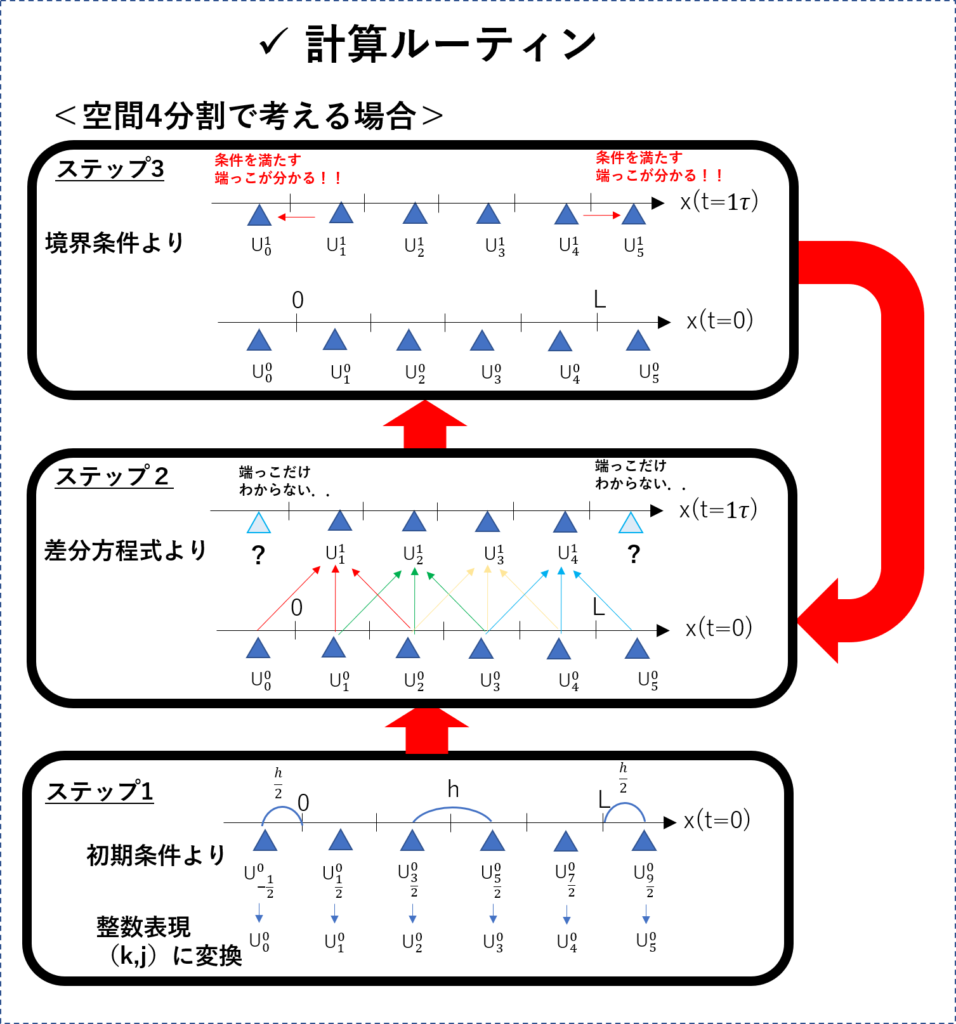
解を求める時刻の上限をTとし、適当な自然数Mを定めて、\tau = T/Mとします。
問題１.１を解くアルゴリズムは次のようになります（ただし、D=1.0とした）。

アルゴリズム

ライブラリのインポート
（１） 変数と初期パラメータを設定
T（時間上限）, M（時間刻み数）, L（空間幅）, N（空間刻み数）, D（拡散係数） を設定する
h = L/N, τ = T/M, α = Dτ/(h^2)　(プログラム中では, τは「tau」, αは「alpha」等とする.)
x[N+2], u[N+2], new_u[N+2]（偏微分方程式の変数をリストとして準備する。）
　
（２） 初期値設定
j := 1,....,N の順に 
    x[j] = (j - 0.5)*h 
    u[j] = 2*x[j]*(1-x[j])
を繰り返す

u[0] = -u[1], u[N+1] = -u[N] 　　（境界条件）

描画する準備
figとaxをつくり、最初の状態のuを描画する。

（３）時間発展を計算
k := 0,1,.....,M-1 の順に 
    （３.１）計算 
    j := 1,2,....,N の順に 
        new_u[j] = αu[j-1] + (1 - 2α)u[j] + αu[j+1] 
    を繰り返す 
    u[1:-1] = new_u[1:-1] （リストの更新） 
    u[0] = -u[1], u[N+1] = -u[N] 　　（境界条件） 
    （３.２）(x[1], u[1]) ～ (x[N], u[N]) を画面に表示 
    (ただし x[0], u[0], x[N+1], u[N+1] は境界処理用なので表示しない) 
    更新されたuを描画 
    plt.pause関数で絵を更新
を繰り返す

アルゴリズム（2時次元ベクトル配列を用いる場合）

ライブラリのインポート
（１） 変数と初期パラメータを設定
T（時間上限）, M（時間刻み数）, L（空間幅）, N（空間刻み数）, D（拡散係数） を設定する
h = L/N, τ = T/M, α = Dτ/(h^2)　(プログラム中では, τは「tau」, αは「alpha」等とする.)

xとtの一次元ベクトルを作成する(np.linspace推奨)

Uの二次元ベクトル用配列を作成する(0詰めする．行は"時間に必要な数"，列は"空間に必要な数"にしておくと楽)
ちなみに
U=np.zeros((3, 4))
と書くと3行,4列の0詰めした2次元ベクトル用配列が作成される．
　
（２） 初期値設定
#初期条件
U[0]=初期条件式   (U[0]=と指定すると"Uの0行目"に一気に値が代入される．列に代入したい人はU[:,0])

#（境界条件）
U[0][0] = -U[0][1], U[0][N+1] = -U[0][N] 　　

（３）時間発展を計算
k := 0,1,.....,M-1 の順に 
    j := 1,2,....,N の順に 
        U[k+1][j] = αU[k][j-1] + (1 - 2α)U[k][j] + αU[k][j+1] (更新式) 
    #（境界条件）
    ここに書く


### 描画する準備 #####
figとaxをつくり、最初の状態のuを描画する。
後は第7回講義の方法でanimation化

このアルゴリズムを実現するプログラムを作成せよというのが当面の課題となります。

課題1

上のアルゴリズムに従ってプログラムを完成させよ。
ただし、T=0.5, M=5000, L=1.0, N=50, D=1.0程度、
初期条件はu(x,0) = 2x(1-x)、境界条件はディリクレ条件とする。

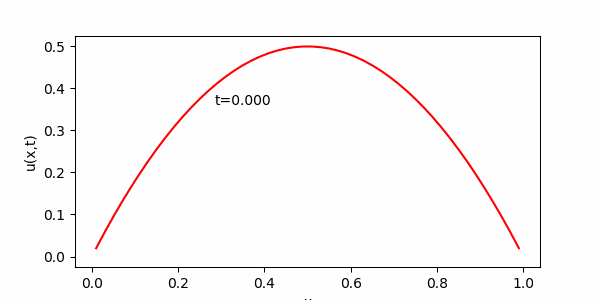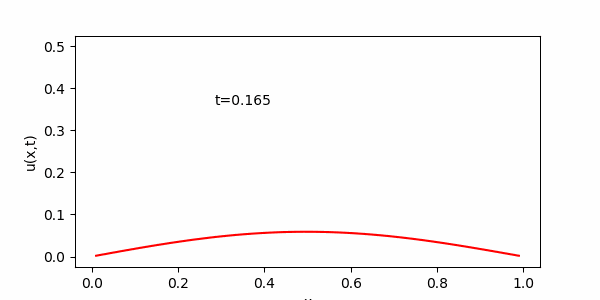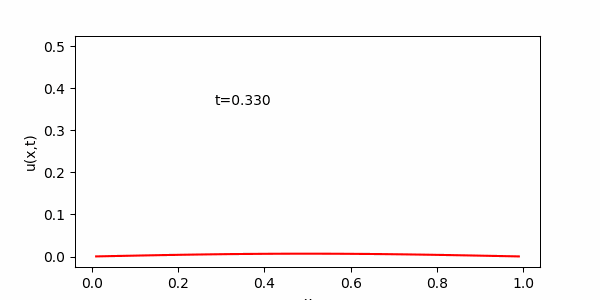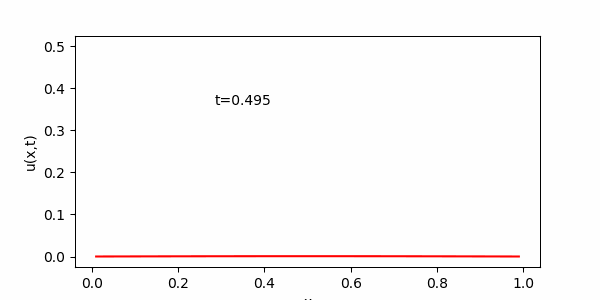
実際の計算部分を正しくプログラムにすることができれば、次のようなアニメーションを見ることができます。
両端から熱（物質）が奪われ、全体の温度（密度）が下がることがわかります。

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です