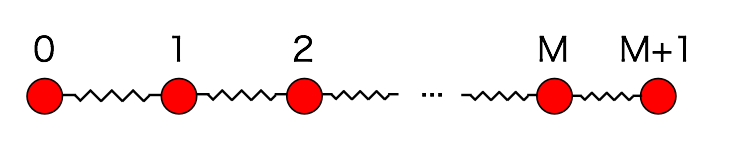
第３・４回（第２週）
今週の目標
グラフを描画する
アニメーションを描画する
簡単な常微分方程式を解いて描画する
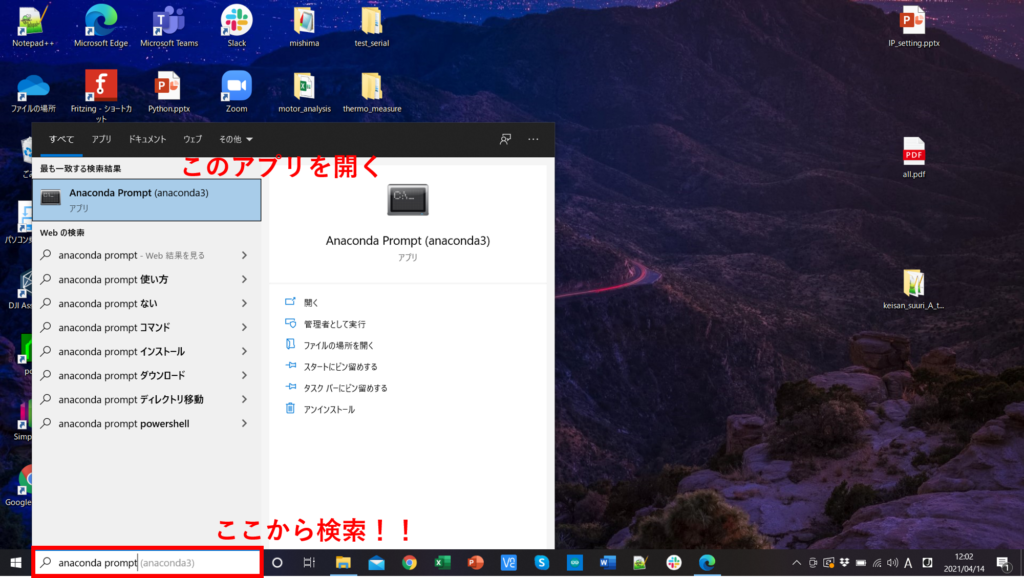
【重要】グラフを別ウィンドウで描画するためのSpyderの設定
特に何も設定していない状態でグラフなどを描画すると、iPythonコンソールの中に描画されます。これでは少々（演習の進行上）勝手が悪いので、別ウィンドウで開くように設定を変えます。
上部にある「ツール」から「設定」を選ぶ
左側の一覧から「iPythonコンソール」を選ぶ
右側上部のタブから「グラフィクス」を選ぶ
右側の「グラフィックのバックエンド」の中の「バックエンド」の項目を「インライン」から「自動」に変更
すぐ下の「OK」
spyderを再起動
Jupyter Notebookを使う人は、このページの最後にある付録を参照してください。
matplotlibによるグラフ描画
先週の演習では基本的なsin関数の描画を行い、まず描画するということになれてもらいました。 今週はmatplotlibで描画する際に必要になる基礎的な知識について学んでいきます。 少しハードルが高いですが、一番大事な情報はmatplotlibのホームページ(matplotlib.org )に書いてありますので、より高度なことをしたくなったら見てみてください。 また、実例を見てみることに勝る教科書はありませんので、どんなグラフがかけるのか興味があれば見てみてください。（https://matplotlib.org/gallery/index.html ）サンプルコードもついているので、そのまま実行すれば手元で遊ぶことが出来ます。
matplotlibの構造
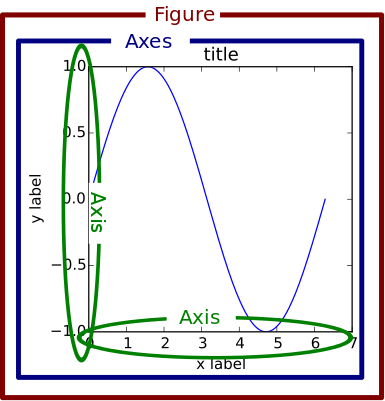
それでは、まず初めにｍatplotlibの描画システムを理解するための基本構造を学びます。 下に示すのは公式ガイドに載っているmatplotlibの描画システムを説明するためのグラフです。
引用：https://matplotlib.org/1.5.1/faq/usage_faq.html 実際にはより複雑なシステムですが、ここでは最も頻度が高く重要な要素に絞って学びます。
※本当は全てオブジェクトと呼ばれていますが、本演習ではオブジェクト指向という考え方について深くは触れません。ひとまずグラフを描いたのちに、グラフ描画の2つの流儀について述べていますので、そちらを参考にしてください。何を言っているのか分からなくても、本演習の進め方には対して影響しませんので、構いません。
早速、コンソール上で以下のようにコマンドを入力してください。
import matplotlib.pyplot as plt
fig = plt.figure()
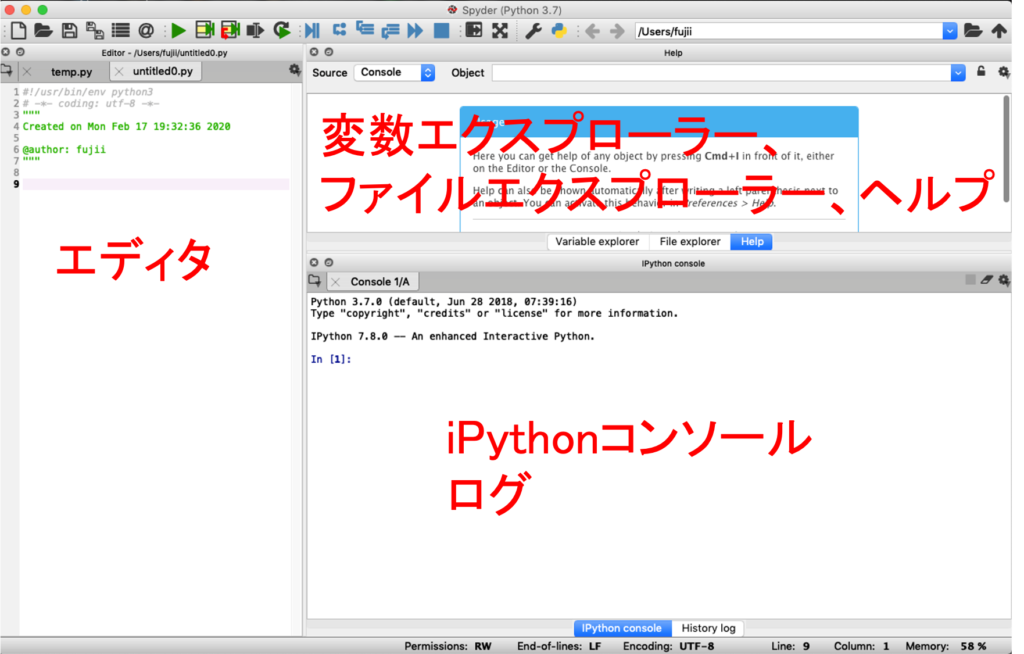
すると以下のような画面になったはずです。
左上にあるような何も描かれていない真っ白なウィンドウが現れたと思います。これがいわばキャンバスであり、Figureの実体になります。 本物のキャンバスは布と木で作られますが、それらがあったとして、いきなりキャンバスをもし作れと言われたら皆さんすぐに作れるでしょうか？絵を描くためのキャンバスには大小様々なものがあり、もし作れと言われたら当然サイズを指定する必要があります。 このFigureという構造も同様です。もちろん何の指示を与えなくてもデフォルトの大きさは与えられていますが。 ここでは示しませんが手元で、次のコマンドを実行してみてください。先のコマンドに比べるとかなり大きなウィンドウが現れたと思います。
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8))
次に、その内側にある構造がAxesについてです。これは、データをグラフにするための座標系に当たります。早速以下のコマンドを実行してみてください。
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
見ての通り真っ白だったウィンドウの中に四角い枠と縦軸、横軸に[0,1]区間の目盛が加えられました。準備されたFigureに座標系を与えることで、数値を図示することが出来るわけです。実はFigureというキャンバスの中には複数の座標系を用意したり、他の字を描くための構造を書くことが出来ます。
※メモ
最後に緑色の円で囲まれているのが、axisという構造です。これは、Axesのそれぞれの軸を示しています。AxesはAxisの複数形で、先にも座標系と書きましたが、二次元か三次元のグラフしか描画しないmatplotlibでは、2つか3つの軸が必要になるので座標系に当たる構造がAxesとなるわけです。 グラフを描く際には、軸の幅や範囲など様々な情報を指定することが必要になります。そのときに最もよく利用して制御する必要がある構造が、このAxisになるわけです。
次にサンプルのための三角関数の数値を準備して、グラフを描くために以下のコマンドを入力してください
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
ax.plot(x, y)
準備されたFigureに座標系を与えることで、数値を図示することが出来るわけです。実はFigureというキャンバスの中には複数の座標系を用意したり、他の字を描くための構造を書くことが出来ます。
グラフ描画の2つの流儀：オブジェクト指向インターフェース vs. pyplotインターフェース
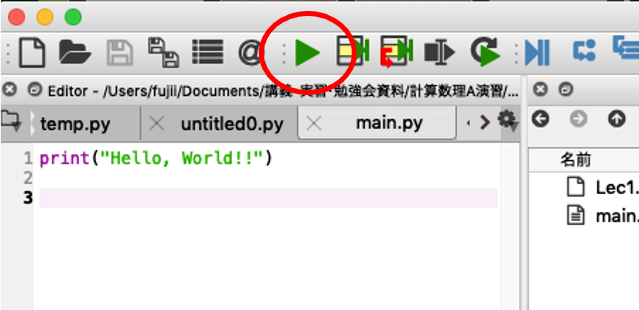
次の2つのプログラムを実行して比較してみましょう。
プログラム1（オブジェクト指向インターフェース）
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
x = np.linspace(0,2*np.pi,101)
y = np.sin(x)
ax.plot(x,y, label="sin(x)")
ax.set_xlabel("x", fontsize=20)
ax.set_ylabel("y", fontsize=20)
ax.legend(loc="best", fontsize=20)
プログラム2（pyplotインターフェース）
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0,2*np.pi,101)
y = np.sin(x)
plt.plot(x, y, label="sin(x)")
plt.xlabel("x", fontsize=20)
plt.ylabel("y", fontsize=20)
plt.legend(loc="best", fontsize=20)
実行してみると、どちらも同じsin波が現れたと思います。 2つのプログラムを比べると、プログラム1に対してプログラム2では大きな違いは2点です。
まずプログラム1では、
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
ax.plot(x, y)
のようにfigやaxというインスタンスを定義し、それらを利用してplotや設定を行います。一方プログラム2では、すべてpltを利用しており、上で説明したようなオブジェクトを有効に利用していません。
また、plt.figure（および第2回で使ったplt.show）というコマンドを消しましたが、問題なくグラフが出てきたと思います。 これはplt.plotという関数が、ひとたび呼び出されれば、細かいことを気にしない代わりに基本設定のまま、空気を読んでグラフを描いてくれる関数だからです。 これによって、plt.figureやax.add_subplotなしにデータをすぐに可視化してくれるわけです。
いずれの方法でも構いませんが、これらのプログラムで描かれたグラフには、自然科学の実験やデータ解析で必要な必要最低限の情報が記載されています。今後レポート課題等はこのように必要な情報が載ったグラフの提出を心がけてください 。 なお，上記プログラム中の”legend”関数についてはこちら のサイトに詳しく紹介しています．
小ネタ：オブジェクト指向？pyplot？
matplotlibとは、Matlabという科学技術計算ソフトの描画システムを真似て作られたもの、と言われています。今回の例の場合、Matlabでは、plt.〇〇の「plt.」を取り除けばそのまま使えるほど、使い方は近いです。ところで最近では、オブジェクト指向が主流になりつつあり、Matlabでもオブジェクト指向での記述が標準仕様になりました（現状は、従来式でも可）。グラフの詳細設定に関しては、オブジェクト指向インターフェースの方が、従来式より有用であることは、MatlabでもPythonでも同様です。おそらく今後は、様々なプログラミングの場面において、オブジェクト指向主義が完全な主流になります。早い段階からオブジェクト指向プログラミングを身につけていくと良いでしょう。
課題1 上のサンプルコードを書き換え、媒介変数表示(x(θ), y(θ)) = (cosθ, sinθ)、0<θ<2πとして、円を描くプログラムをかけ。
オブジェクト指向インターフェースによる描画の詳細設定
このやり方は、先のmatplotlibの構造を説明を行うときに用いた方法で、このやり方がmatplotlibの基本的なグラフ描画方法だと考えてください。 大まかな流れは、先ほど説明したようにFigureを作り、座標系となるAxesを準備して、データを描くことになります。
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
ax.plot(x, y, label="sin(x)")
ax.set_xlabel("x", fontsize=20)
ax.set_ylabel("y", fontsize=20)
ax.legend(loc="best", fontsize=20)
plt.show()
線の色・線のパターンの変更
matplotlibではデフォルトのグラフの色として、青色が選択され、線で結ばれてグラフが描画されます。 ここでは、任意の色に変更したり、点線にしたりしてみます。 変更方法はとても簡単で、上のサンプルコードのax.plotに以下のように追加するだけで変更できます。
ax.plot(x, y, "r--", label="sin(x)")
この例にあるようにしてもう一度グラフを描くと、赤い点線でグラフが描かれたと思います。matplotlibのplot関数では、データとなる二つの配列を与えた後に、文字列を書き込むことでグラフの色と線の種類を選択することが出来ます。 色は次に示す省略した文字で指定し、線の種類は記号の組み合わせで指定します。 基本的には、”[色][線の種類]”という構造になっています。 一文字のアルファベットで指定できる色には、 ‘b’（青）, ‘g’（緑）, ‘r’（赤）, ‘c’（シアン）, ‘m’（マゼンダ）, ‘y’（黄）, ‘k’（黒）, ‘w’（白） があります。
次に線の種類を変更するには、一文字のアルファベットのあとに記号の組み合わせで指定できるのですが、簡単に指定できるものとして ’-‘, ‘–‘, ‘-.’, ‘:’ があります。それぞれ試してみて線の種類を見てみてください。 （https://matplotlib.org/gallery/lines_bars_and_markers/line_styles_reference.html ）
色も種類もより高度な方法を用いれば細かな設定が可能ですが、ここではあまり高度な内容は必要ないので、興味がある人はマニュアルページを見てみてください。
参考： Specifying Colors (https://matplotlib.org/tutorials/colors/colors.html#sphx-glr-tutorials-colors-colors-py ) Linestyles (https://matplotlib.org/gallery/lines_bars_and_markers/linestyles.html )
マーカーのプロット
線の種類はデータ間をつないで可視化しました。ここでは、そのデータ点自体を描画する方法を学びます。数値計算ではあまり表だって使うことはないかもしれませんが。
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
ax.plot(x, y, "o", label="sin(x)")
ax.set_xlabel("x", fontsize=20)
ax.set_ylabel("y", fontsize=20)
ax.legend(loc="best", fontsize=20)
plt.show()
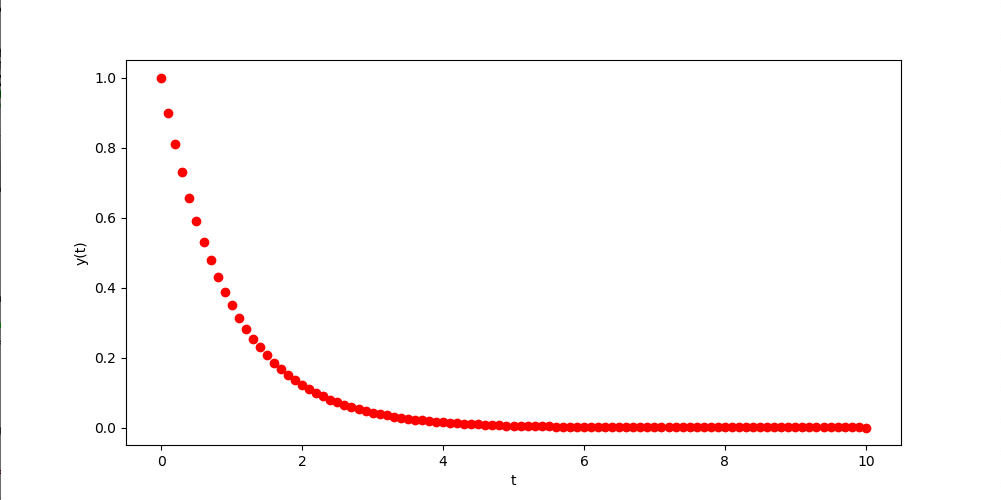
サンプルコードを実行すると先ほどまでつながれていた線が消えて、データとしてxとyにあるデータ自体が点として描かれています。x軸方向は等間隔でもy軸のデータが山の頂点に近づくにつれて詰まっているのがよくわかります。 ここでは、プロットするタイプとして”o”（アルファベットのオー）を指定しました。線の種類と同様に他にもプロットの種類があります。 種類がかなり多いので、リンク先のmatplotlibのマニュアルページを参照してください。（https://matplotlib.org/gallery/lines_bars_and_markers/marker_reference.html ） また、これはデータ点自体のある場所にプロットしているだけなので、データ間をつなぐ線は独立に描くことが出来ます。
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
ax.plot(x, y, "o-", label="sin(x)")
ax.set_xlabel("x", fontsize=20)
ax.set_ylabel("y", fontsize=20)
ax.legend(loc="best", fontsize=20)
plt.show()
描画範囲の指定
それでは次にグラフを描く範囲の指定方法を学びます。 特に指定しなければ、サンプルコードにあるようにデータを全て描ける範囲を自動で取ってくれます。 ここでは、あえて描画する範囲を絞って見ます。
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
ax.plot(x, y, label="sin(x)")
ax.set_xlim([0,2.0*np.pi])
ax.set_ylim([-1.0,1.0])
ax.set_xlabel("x", fontsize=20)
ax.set_ylabel("y", fontsize=20)
ax.legend(loc="best", fontsize=20)
plt.show()
このサンプルコードでは、描画するサイン関数がぴったりはまるように範囲を指定しました。]
ax.set_xlim([0,2.0*np.pi])
ax.set_ylim([-1.0,1.0])
上ののコードがそれぞれax.set_xlim,ax.set_ylimが、x軸、y軸の範囲を制限しています。x軸y軸どちらを指定するかは見ての通りxlimかylimかの違いで使い方は全く同じです。 関数の引数に与えるリスト[a,b]でaが軸の下限値、bが上限値を表しています。 サンプルコードでは、元のコードにあった余白がなくなっていることがわかると思います。
課題2 先のサンプルコードにおいて、x=0, x=π近傍を拡大して直線的に見える様子を確認せよ。
円を描く
図形を描くことはいろいろな場面で必要になるかと思いますが、matplotlibには基本的な図形を描けるようにモジュールが用意されています。これを使えば色々と図形を描くことが簡単にできるのですが、簡単な円を描くだけであればplot関数を用いて出来ますので、その方法を学びます。また多角形の枠の作り方も学びます。
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
cx = 0.0
cy = 0.0
ax.plot(cx, cy, 'o', markersize=200.0)
ax.set_xlim([-0.5, 0.5])
ax.set_ylim([-0.5, 0.5])
ax.set_xlabel("x",fontsize=20)
ax.set_ylabel("y")
ax.legend(loc="best")
plt.show()
これまでのplot関数に与えるデータはそれぞれいくつかの値を持つ配列だけでしたが、上のサンプルコードにあるようにそれぞれ一つのデータでもグラフを描くことができます。この場合データ間をつなぐ線の種類を指定しても一点しかデータがないのでつなぐことが出来ず、何も描かれません。そこで、データ点自体を描画するマーカーを指定してその座標点のデータを描画しています。ただし、折れ線グラフのようにデータをプロットしながら線を結ぶことを想定しているので、マーカーは線の太さよりも少し太いくらいです。なので、何かしら円を描くつもりでマーカー機能を使う場合には、サイズを大きくする必要があります。
課題3 ビリヤードのナインボールの初期配置のように9個の円で四角形を作れ。（向きは好きにしてください。）
多角形を描く
多角形は線をつなげばいいので、四角形は以下のようにすれば出来ます。
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
x = np.zeros(5)
y = np.zeros(5)
for i in range(5):
x[i] = np.cos((i*2.0*np.pi/4.0)+np.pi/4.0)
y[i] = np.sin((i*2.0*np.pi/4.0)+np.pi/4.0)
ax.plot(x, y, "-")
ax.set_xlabel("x", fontsize=20)
ax.set_ylabel("y", fontsize=20)
ax.axis('scaled')
ax.set_aspect('equal')
ax.legend(loc="best", fontsize=20)
plt.show()
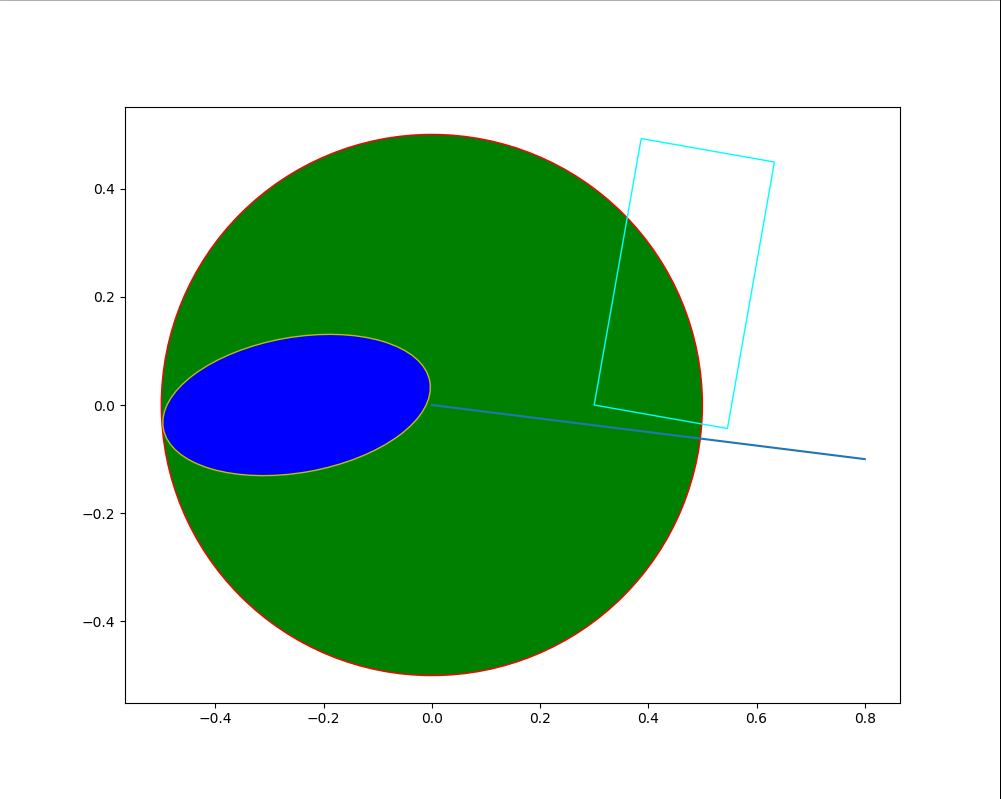
matplotlibでは以下のようにいくつかの図形を簡単に描けるようになっています。 描くためのモジュールがpatchesで以下のサンプルコードにあるように必要な場合にインポートしてください。
import matplotlib.patches as patches
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
# 円を作る
c = patches.Circle(xy=(0, 0), radius=0.5, fc='g', ec='r')
# 楕円を作る
e = patches.Ellipse(xy=(-0.25, 0), width=0.5, height=0.25, angle=10, fc='b', ec='y')
# 長方形を作る
r = patches.Rectangle(xy=(0.3, 0), width=0.25, height=0.5, angle=-10, fc='#00FFFF', ec='#00FFFF', fill=False)
# 作った図形を座標系の中へ描く
ax.add_patch(c)
ax.add_patch(e)
ax.add_patch(r)
# 二点の座標データを直接指定して直線を引く
ax.plot([0, 0.8], [0, -0.1])
ax.axis('scaled')
ax.set_aspect('equal')
実行するとこんな感じです。
課題4 多角形として、六角形と八角形を描け。可能であればn角形を描けるプログラムを作れ。
より良いグラフを作るために
任意の場所に文字を書く
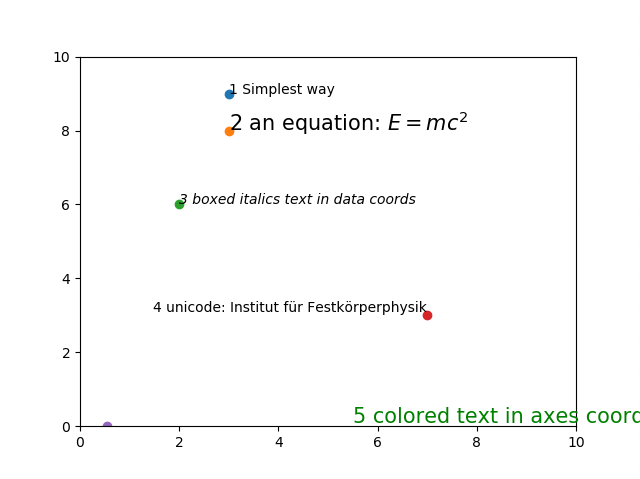
次にグラフをよりよく説明するために必要な文章をグラフ内に書く方法を学びます。 ax.plot関数がデータを書き出すための関数でしたが、文字を描くにはax.text関数を使います。基本的なルールは、 ax.text(左下のx座標, 左下のy座標, [文字列]) のように文字を書き出す地点を指定して、次に書きたい文字列を書きます。
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.text(3, 9, '1 Simplest way')
ax.plot(3, 9, 'o')
ax.text(3, 8, r'2 an equation: $E=mc^2$', fontsize=15)
ax.plot(3, 8, 'o')
ax.text(2, 6, '3 boxed italics text in data coords', style='italic')
ax.plot(2, 6, 'o')
ax.text(7, 3, r'4 unicode: Institut für Festkörperphysik', verticalalignment='bottom', horizontalalignment='right')
ax.plot(7, 3, 'o')
ax.text(0.55, 0.01, '5 colored text in axes coords', transform = ax.transAxes, color='green', fontsize=15)
ax.plot(0.55, 0.01, 'o')
ax.axis([0, 10, 0, 10])
plt.show()
当然axは座標系を作るために呼び出したので、ax.textにまず初めに書き込む座標はこの座標系上での値になります。set_xlimなどを使い描画する範囲を指定するためには、text関数に入力する座標がその範囲に収まっている必要があります。 サンプルコードを順に見ていきましょう 1つ目の書き方が基本形です。特に指定することもないのであれば、これで十分です。 2つ目の書き方は、LaTeXコマンドを使う方法です。文字列は””か”で包めば文字列と認識されるのですが、その前にrとつけておくとLaTeXコマンドが利用できます。加えて、ラベルの指定と同様にfontsizeで文字の大きさを指定できます。 3つ目の書き方は、文字のフォントスタイルをstyle=’italic’とすることで斜体へ変更しています。 4つ目の書き方は、これまで座標位置が必ずテキストの左下だったものが、テキストの右下に変わっています。 これはverticalalignment=’bottom’, horizontalalignment=’right’によるもので、verticalalignmentには{‘center’, ‘top’, ‘bottom’, ‘baseline’, ‘center_baseline’}が指定でき、horizontalalignmentには{‘center’, ‘right’, ‘left’}が指定できます。 5つ目の書き方は、これまでのものと少し違います。上記の4つのtextでは、初めの座標がテキストの左下の位置と対応していることを見るためにax.plotで点を同じ座標に打っていて、ちゃんと左下角にあることが見て取れていると思います。しかし、最後のものだけ一致していません。 これは、後ろの方に書いてあるtransform=ax.transAxesというコマンドのためです。これを行うとaxによって作られた座標系の中の位置ではなく、figure全体に[0,1]×[0,1]の座標系 があるような、絶対的な位置により指定されることになります。
グラフへの数値の描画
本演習を通して数値を表せる必要があるので、数値を文字列として書き出す方法を述べておきます。 いくつかやり方はあるのですが、format形式が私の知る限り一番便利なのでその方法を示します。 format形式では、以下のようにint型やfloat型の変数を文字列変換します。これを行うと表示だけでなく、ファイル名として保存するときにもパラメータの数字が入ったファイル名を連続して呼び出すことが出来ます。
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
a = 2.3
b = 5
print(f'Format Style: a = {a}, b = {b}')
ax.text(3, 2, f'Format Style: a = {a}, b = {b}')
a = 2
b = 1
ax.text(a, b, f'Format Style: a = {a}, b = {b}')
ax.axis([0, 5, 0, 5])
plt.show()
これまでと違うのは文字列の”もしくは””の前にfを付け加えることと、文字列に変更したい変数を{}で囲うことです。 print関数で文字列を書き出す場合でも、ax.text関数でグラフに書き出す場合でも文字列として数値が出ているのがわかると思います。 format形式だと最後の例のように変数の値を変更すると数値が変更されていることがわかると思います。
小ネタ：print関数再訪
上の例で、format形式を学びました。その上で、以下の例を見てみましょう。
a = 1
b = 2
print('a = ', a, ', b = ', b, sep='')
print(f'a = {a}, b = {b}')
実行してみるとどうでしょうか？a = 1, b = 2が2回出てきたと思います。3行目は第2回で学んだやり方、4回目は今回学んだやり方ですが、結果に違いはありません。 では、この形式、つまり、
ax.text(3, 2, ['a = ', a, ', b = ', b])
と置き換えたらどうなったのでしょうか？（※ sep=”を含めるとエラーになるので、あらかじめ消しています。） print文で同じ結果だったので…？それとも…？ 実際にどうなるか自分で確かめてみてください。
複数のグラフを一つの画面に描画する
複数のデータを一つのグラフ上にプロットするには以下のように二つの座標系を準備します。 fig.add_subplot(111)で一つの座標系をFigure全体に描画していました。ここでは書き込む座標系を二つにします。そのためにadd_subplotの引数について、以下のサンプルコードを読んでもらった後説明します。
fig = plt.figure(figsize=(10,8))
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
y2 = np.cos(x)
ax1.plot(x, y, label="sin(x)")
ax1.plot(x, y2, '--', label="cos(x)")
ax1.set_xlabel("x", fontsize=20)
ax1.set_ylabel("y", fontsize=20)
ax1.legend(loc="best", fontsize=20)
ax2.plot(x, y2, '--', label="cos(x)")
ax2.set_xlabel("x", fontsize=20)
ax2.set_ylabel("y", fontsize=20)
ax2.legend(loc="best", fontsize=20)
plt.show()
fig.add_subplot(211)にある謎の211という数字の組み合わせですが、実はこの部分は以下のように書き換えることが出来ます。fig.add_subplot(2,1,1)
意味としては(行数,列数,場所)となりつながった三桁の数字も同じ意味です。 行数、列数によってFigureを縦横に必要な分だけ分割して、その中でどの領域に座標を設定するかを最後の数字で指定しています。分割された領域は行優先で数が割り振られています。 例えば、fig.add_subplot(3,4,10)という指示を出すと、ちょうど10の当りにだけ座標系が設定されます。 注意すべきは、分割した全ての領域を利用する必要はなく、あくまで作りたい座標系のサイズと位置を決めるだけです。なので、適当に与えるとグラフが重なってしまうので注意してください。
課題5 上下にグラフを分割して、上に任意の二次以上の多項式関数のグラフを描き、下段にその導関数のグラフを描け。定義域は0<x<3とする。ただし、導関数は数値的（近似的）に求めよ。
matplotlibでのアニメーション
この授業の範囲で手軽にアニメーションの描画を行う方法には、以下の方式で十分です。ただし、matplotlibのanimationの関数を使ったより高速な方法もあります。下の方に付録として記載しておくので、余力がある人は見てみてください。
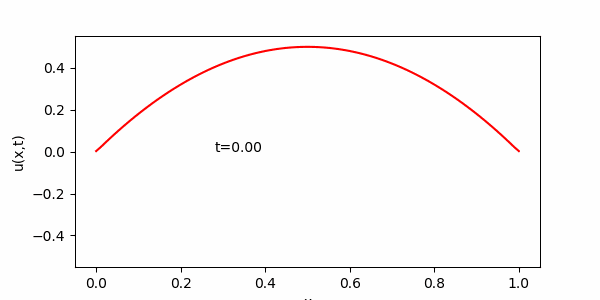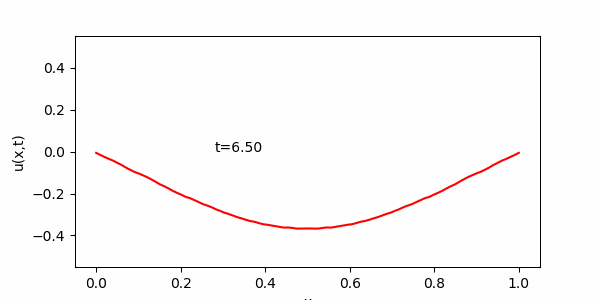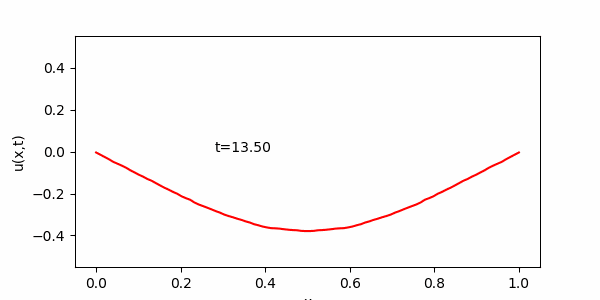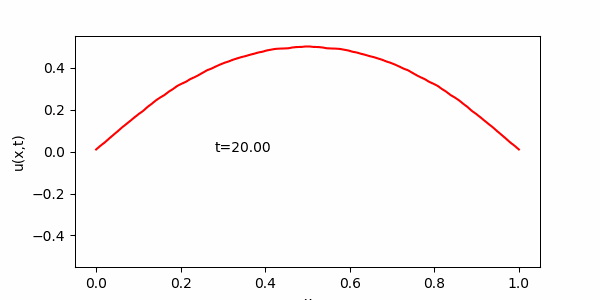
この演習でメインに用いる方法は、一度描いたグラフのデータを更新することでアニメーションを作る方法です。題材として進行波を描くプログラムを用意したので実行してみてください。
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
x = np.arange(0, 10, 0.1)
y = np.sin(x)
dt = 0.05
v = 1.0
lines, = ax.plot(x, y, "r")
for i in range(50):
t = dt * i
y = np.sin(x - v*t)
lines.set_data(x,y)
plt.pause(0.01)
plt.show()
グラフのデータが、line.set_data(x,y)の部分で更新されます。 グラフ自体の実態としてlineがまず、line, = ax.plot(x, y, “r”)によって作られています。ax.plot関数はグラフを描くと同時に、関数として描かれたグラフに関する様々な情報をreturnしてくれます。ここでは詳細に触れませんが、その中でlineとして受け取ったものをこの例題の様に制御するとグラフが変わることだけ覚えておいてください（気になる人は、変数エクスプローラーの歯車をクリックし、「Exclude unsupported data types」のチェックを外すと、linesの中身を見ることができます）。
このデータを更新するだけではグラフの描画は変更されないので、その次の行にあるplt.pause(0.01)によりグラフは更新されます。0.01は更新された後にそのまま何秒待つかを指定しています。変えてみてアニメーションの進む速度がどう変わるのか確かめてみてください。
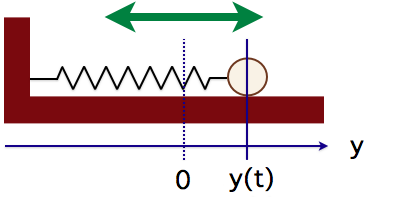
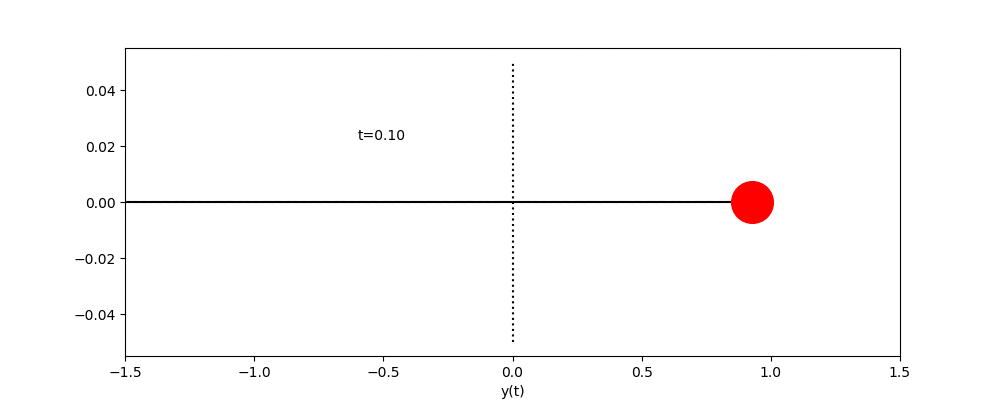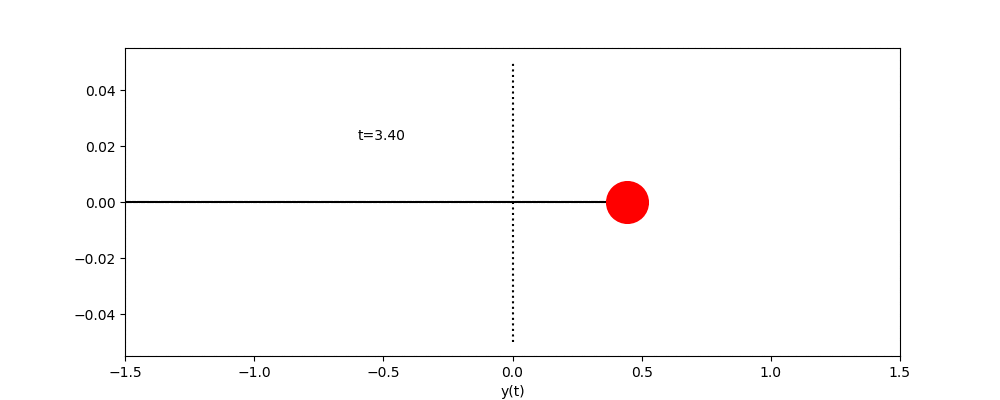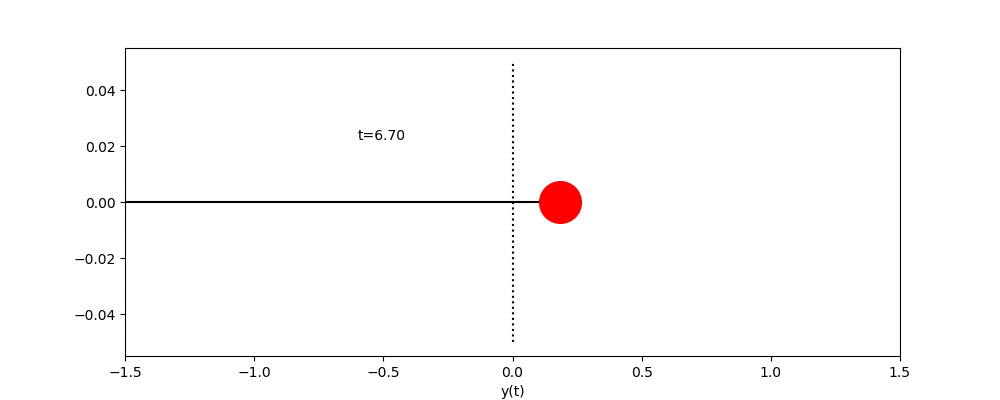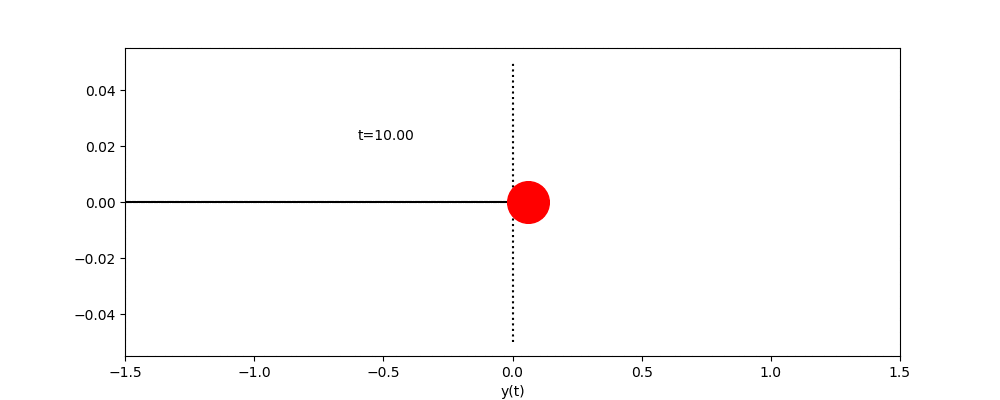
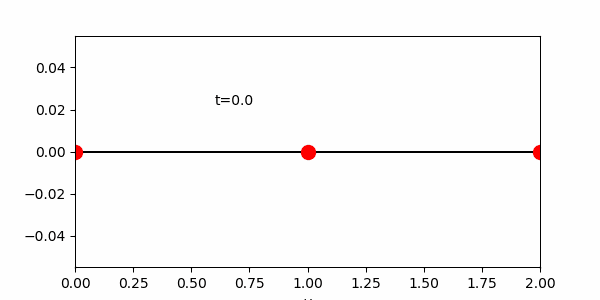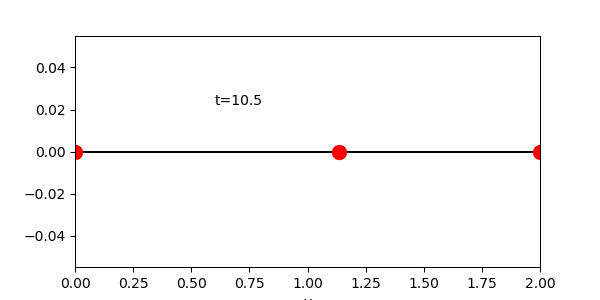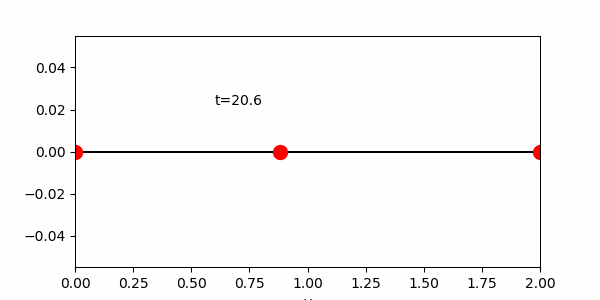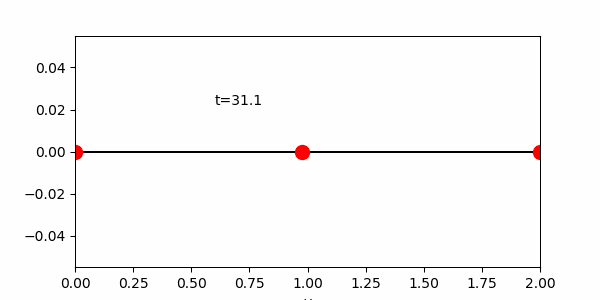
練習 円がx軸上を0から10まで移動するアニメーションを作れ。
（ラインの更新方法については述べたが，patchの更新方法については紹介していない．
例えば
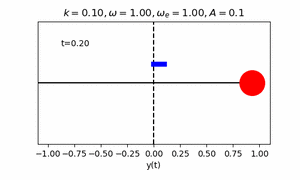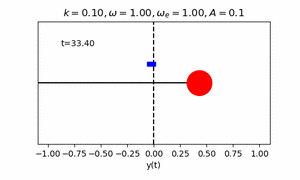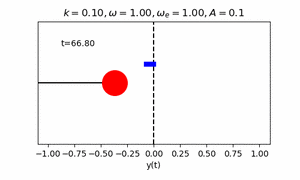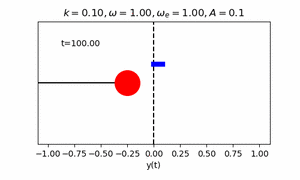
課題6 いずれかの方法を用いて、中心座標に円を描きその周りを円が公転するアニメーションを作成せよ。
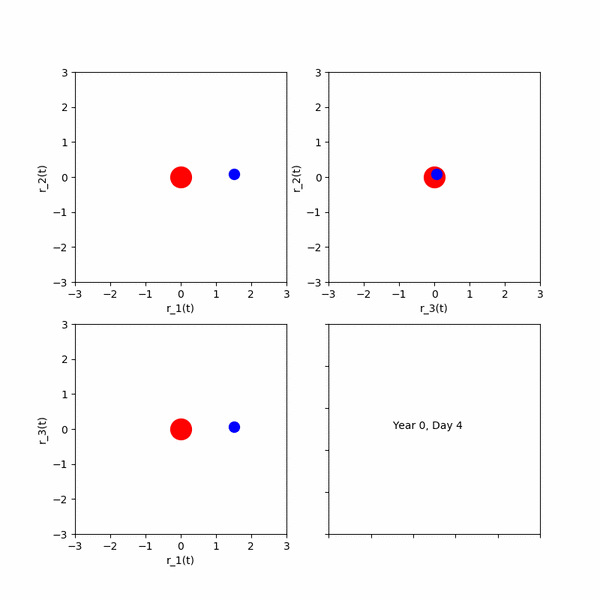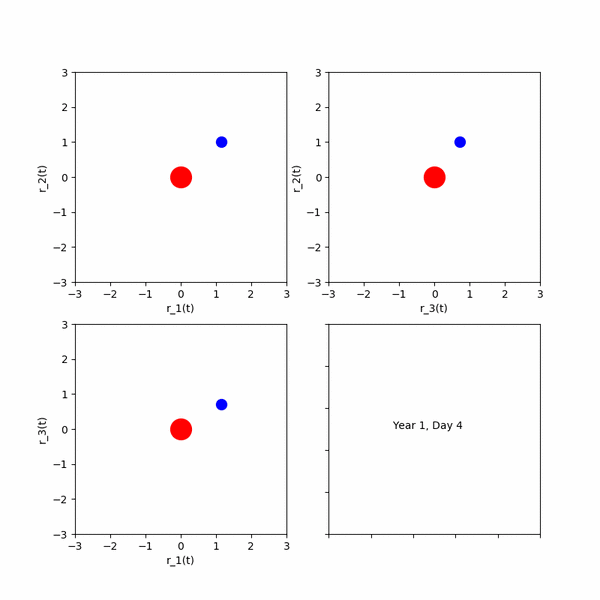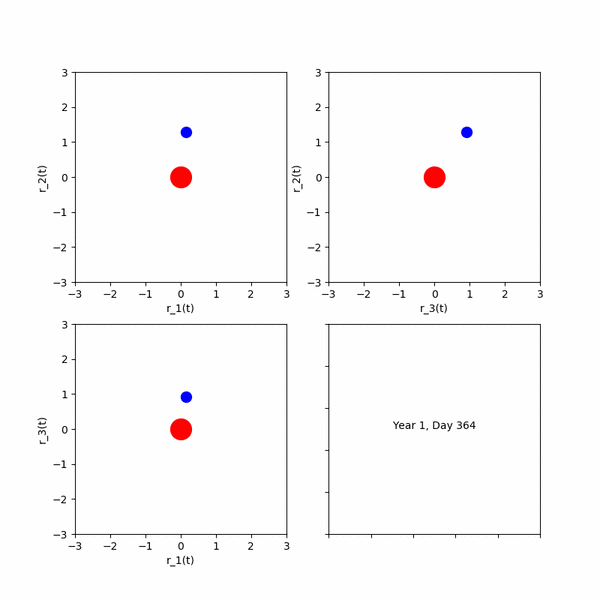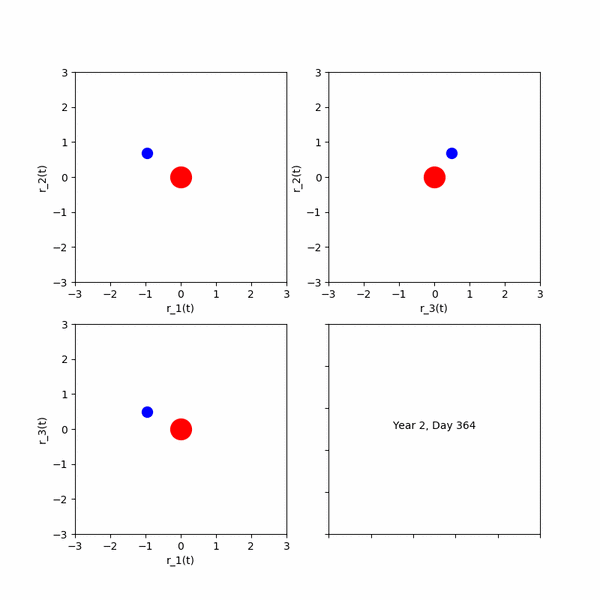
エクストラ課題 1課題6の公転する円を中心に，さらに一つ公転する円を描き（太陽，地球，月のような円を描き）アニメーションを作成せよ。その後，任意の円の数Nを入力すると，連鎖公転する円が描けるプログラムへ拡張せよ．ただし，各円の公転の角速度は（2π,4π,・・・2Nπ）となるものとする．（初期位相phaiはすべて0とし，公転軌道半径は任意のもので構わない．）
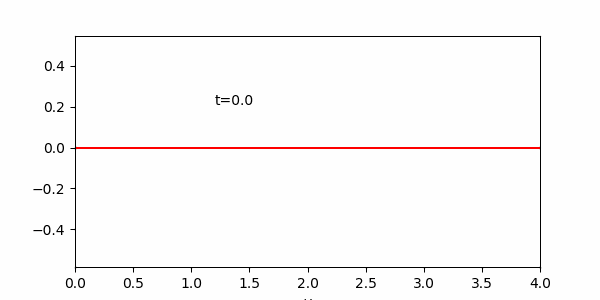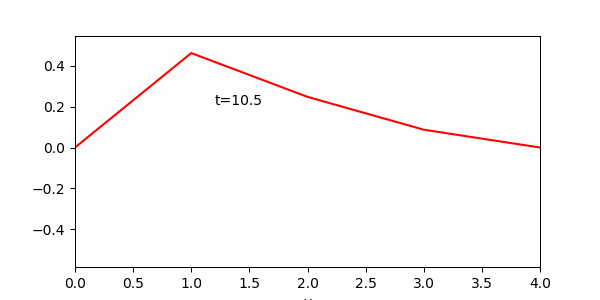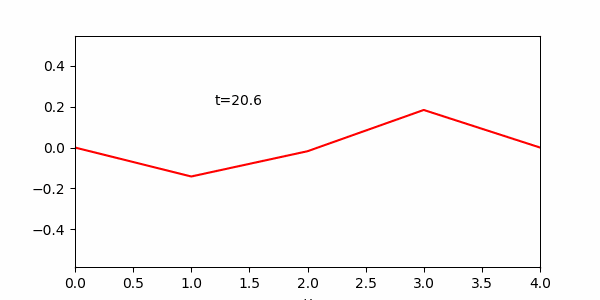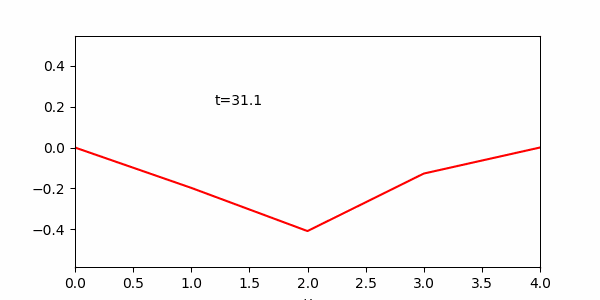
エクストラ課題2 エクストラ課題1で作成した”最後に生成される円”の軌道をアニメーション図中に併載させよ（軌道描画はアニメでなくても構わない）。この際，図の縦軸は”y”，図の横軸は”x”とする
エクストラ課題 3エクストラ課題2で描いた軌道および時間を基に，横軸が時間”t”，縦軸が”y”のアニメーション図(または，静止グラフ)を別途作成せよ。
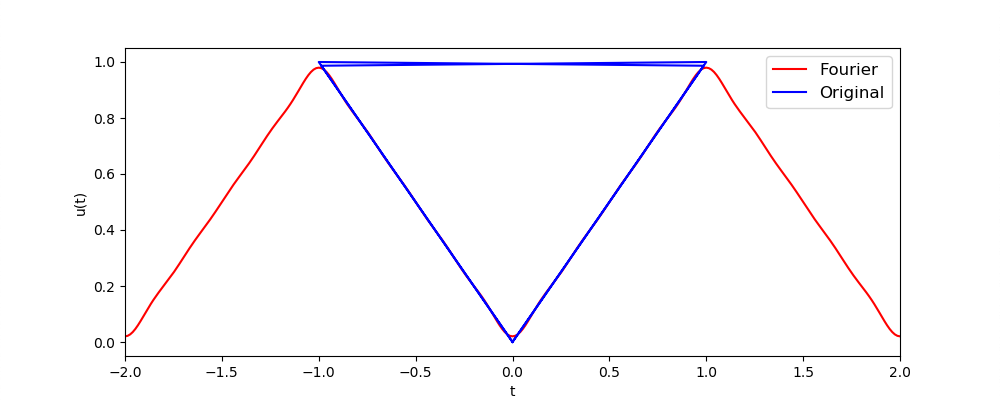
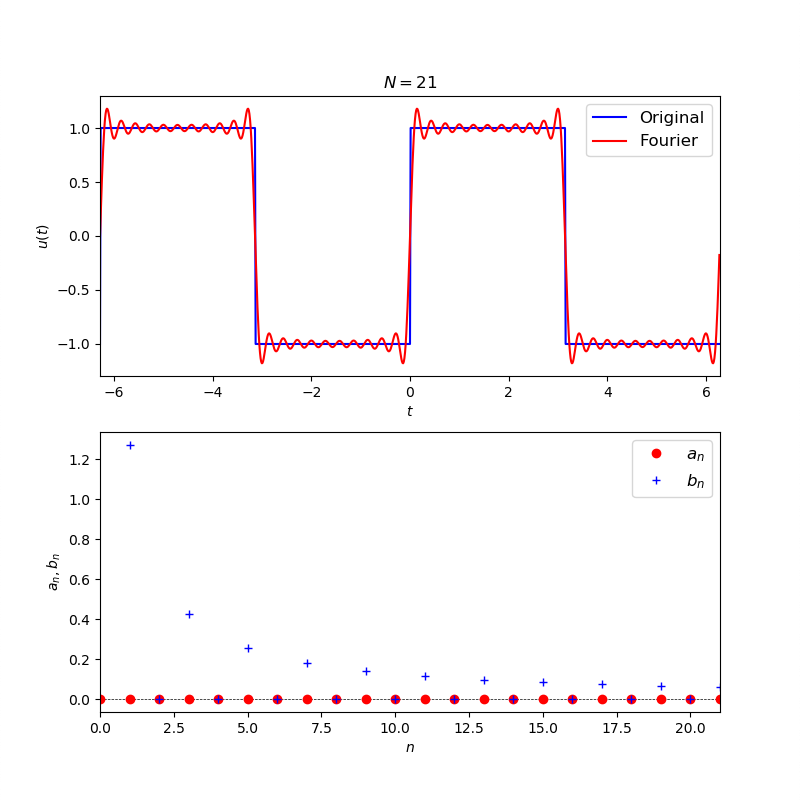
エクストラ課題 4エクストラ課題3で，描いた軌道が近似的に矩形関数 – Wikipedia のような形にできるのか，またできるとしたら軌道半径・回転の角速度・初期位相をどのようにすれば良いか，考えよ。
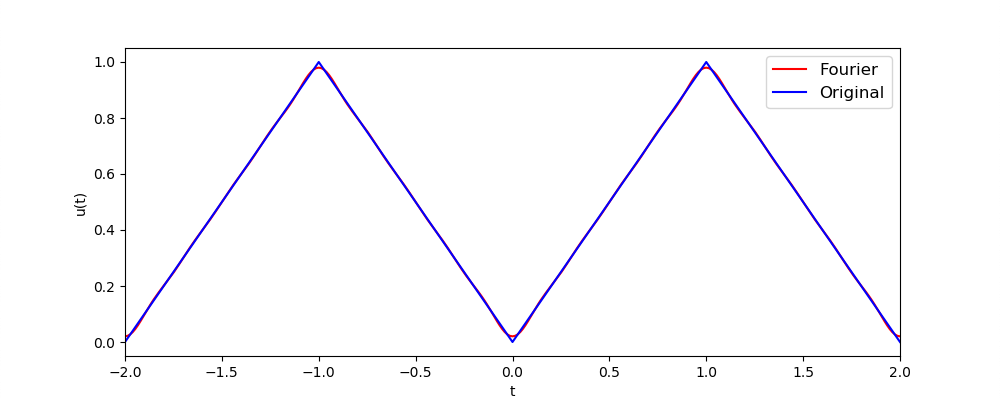
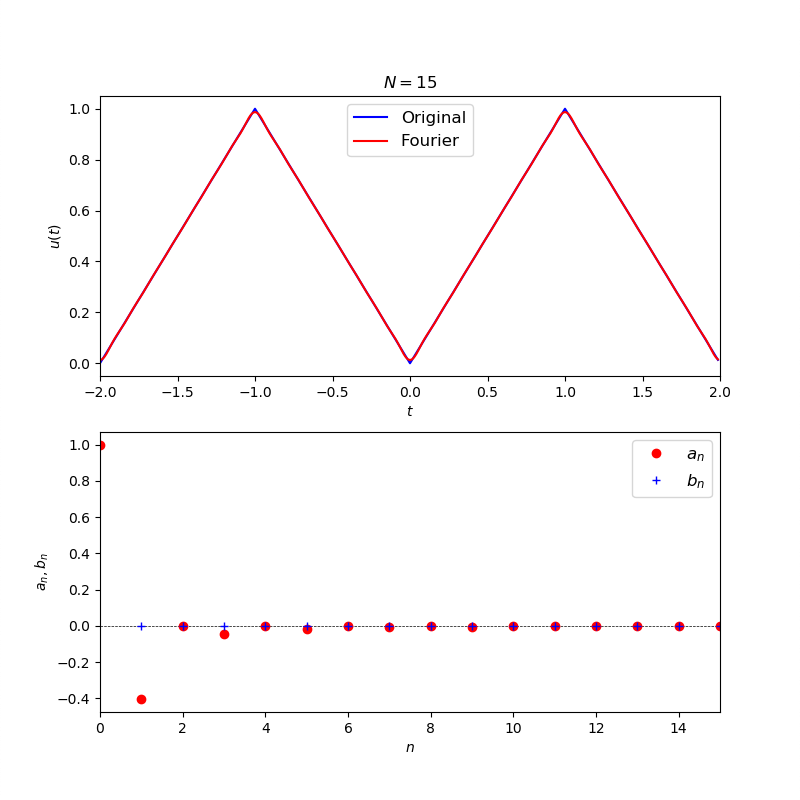
エクストラ課題 5エクストラ課題4で矩形波を描けた原理を理解し，この動画 を見て，連鎖公転円系を2軸分用意して任意の図形（ハートやミッキーなど）を2次元平面上に描画するプログラムを作成せよ(動画の2:40秒あたりに再生されているものを作る)。ただし，ハートを描くための関数はこちら を参照．（手順ヒント：①まずは2次元平面上に一筆書きの 目標図形を描き，x座標用配列,・y座標用配列に値を格納する．②x座標用配列,・y座標用配列と同じサイズの時間t用配列を作成する．③得られた配列x(t), y(t)に対してそれぞれ フーリエ級数展開 を実装し，フーリエ係数を手に入れる．この際，同じ周波数成分のsinとcosのフーリエ係数から，位相差，および，ノルムを算出しておく．⑤得られた位相差・ノルム・周波数が公転系の何を意味するのかを考えてx軸用，y軸用の公転系をそれぞれ実装する．）
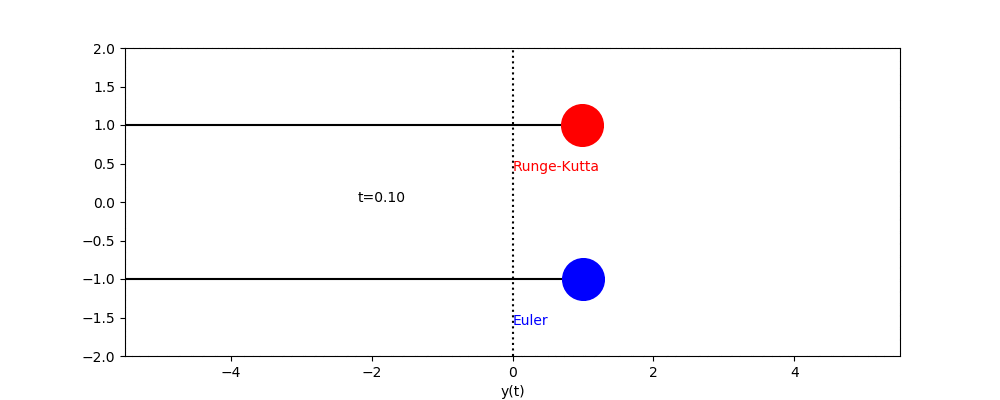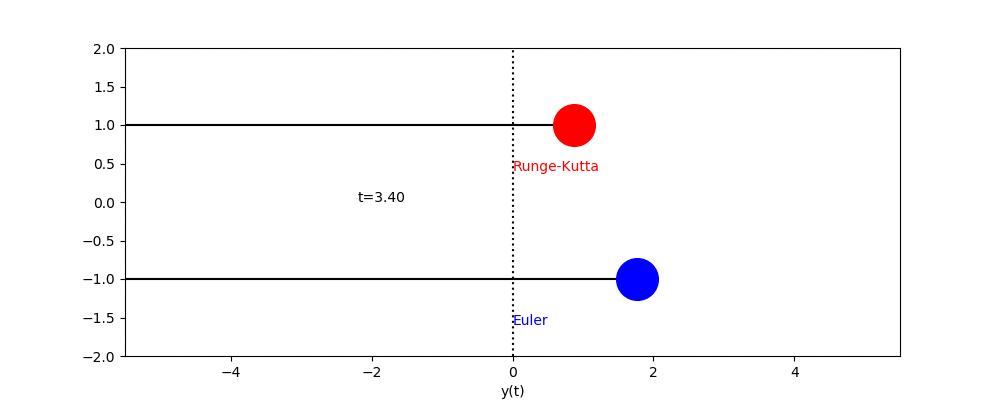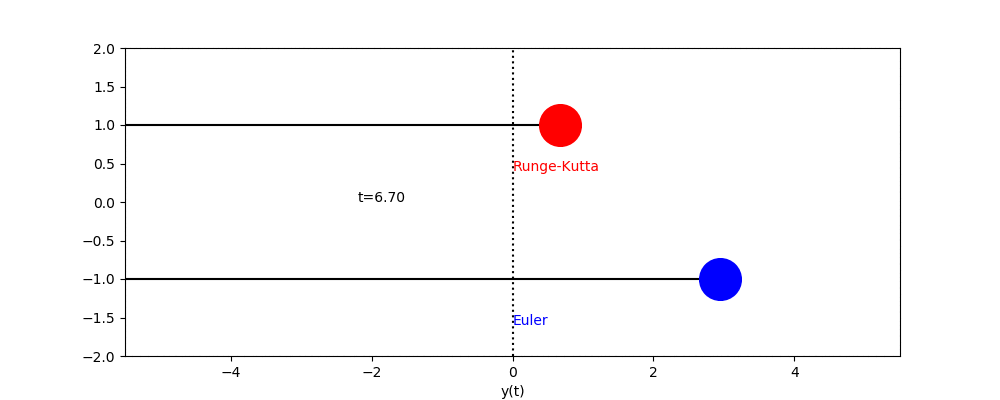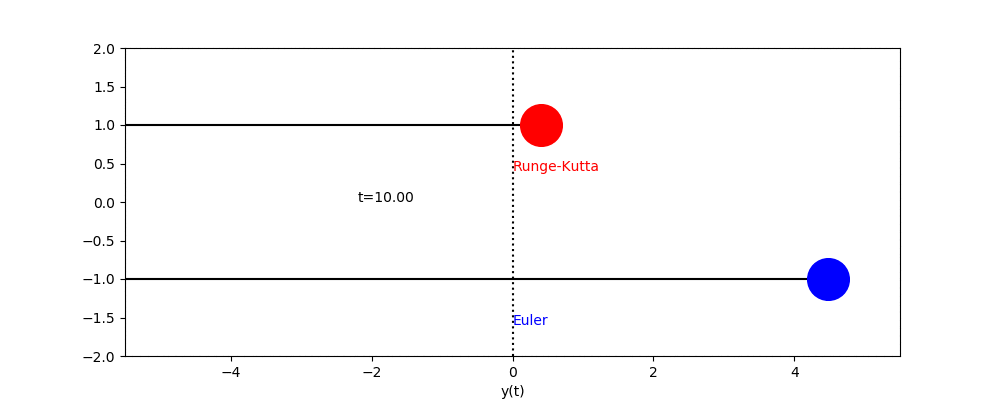
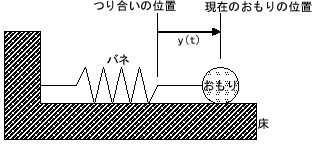
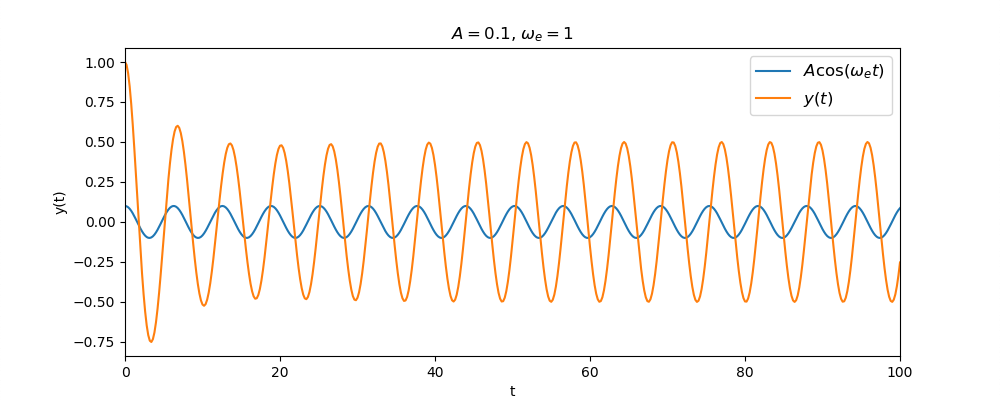
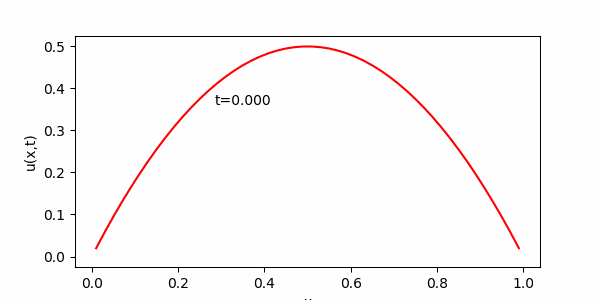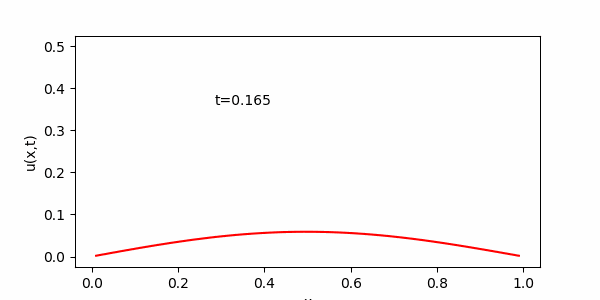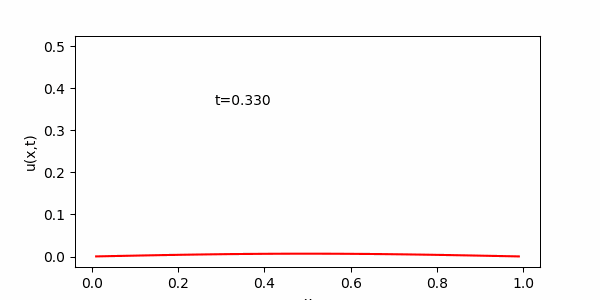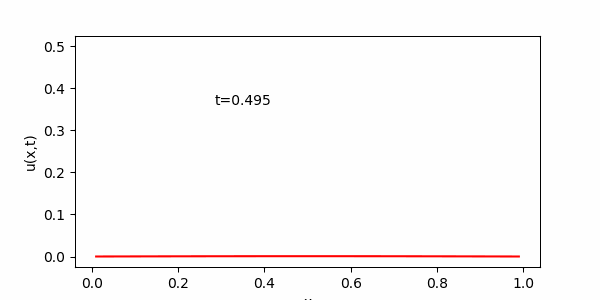
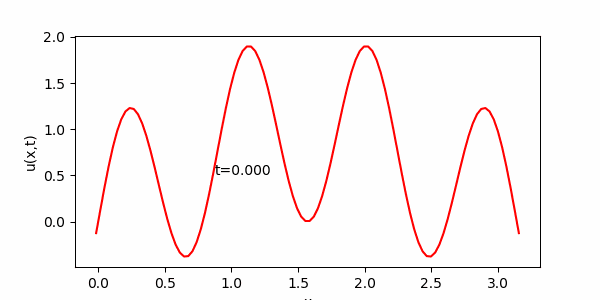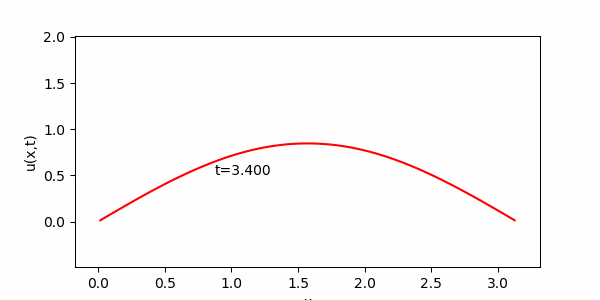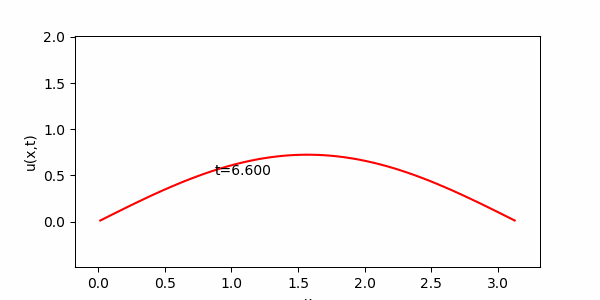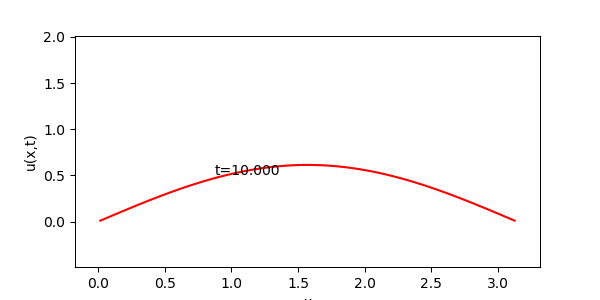
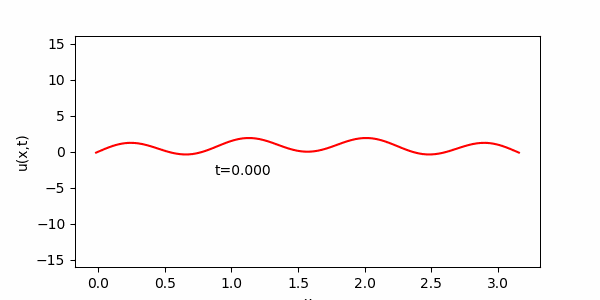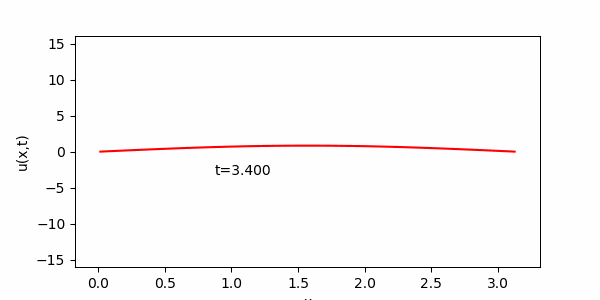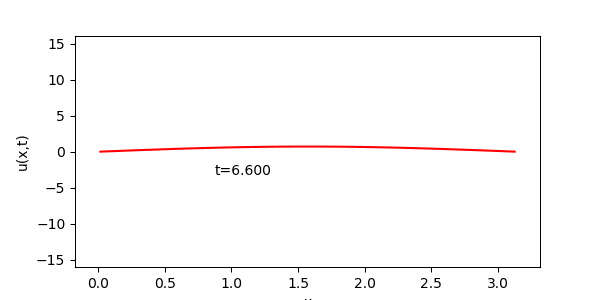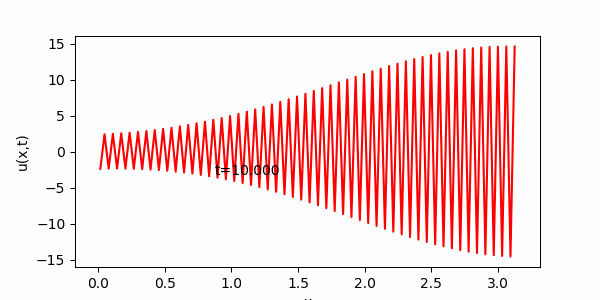
簡単な常微分方程式とその解のグラフ化
今日は、計算数理Aの講義に出てきた次の常微分方程式を用いて演習を進めます。この方程式は、講義で詳しく説明されたと思いますが、例えば放射性同位体の崩壊を記述するモデル方程式として導出されます。講義で紹介があったように、例えば放射性炭素による年代測定にはこういった微分方程式が役立ちます。$N(t)$を時刻$t$ における放射性同位体の原子数とすると下記のような微分方程式が得られることは講義で見たとおりです。
(P)
\[\left\{
さて、この微分方程式は簡単に解けて、解は次のようになることも講義で見ました。
(S)
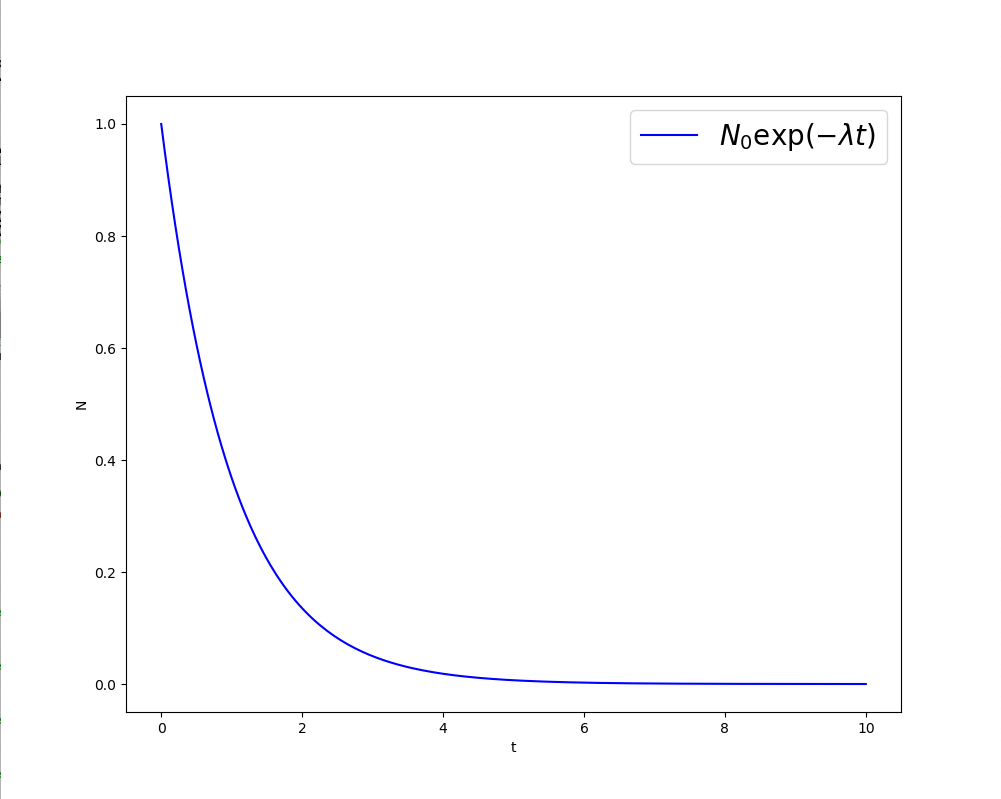
今日の目標は、解(S )をグラフとして表示するプログラムを作成することです。パラメータ$\lambda$および$N_0$を与えれば、( S )のグラフをかけるはずです。 実は前回の内容で $y= sin(x) $のグラフを描いてもらいましたが、前回の$y= sin(x) $を描く方法を記述した部分にしたがって、(S )のグラフを描いてください。
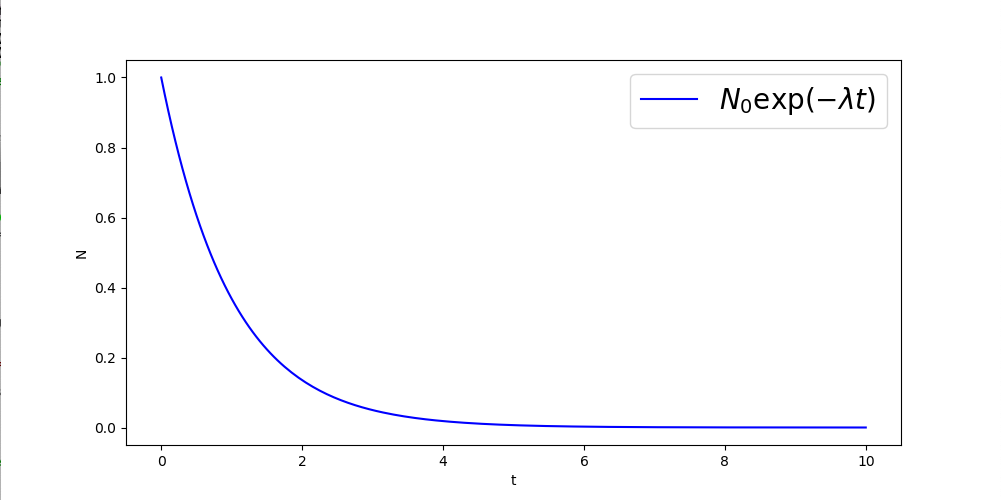
課題7 $ N(t) = N_0e^{- \lambda t} $のグラフを描け。ただし、$N_0 = 1, \ \lambda = 1,\ \ 0 \leq t \leq 10$とする。
課題8 課題7の式において、$N( \tau ) \ \ = \ \ 0.5N_0 $となる$\tau$（半減期といいます）を手計算で求めよ．ただし，$\ \lambda = 1$とする．
答え：$ \log 2$ (約0.693)
課題9 課題7で作成したプログラムを用いて課題8の$\tau$を近似的に次のような手法で求めたい。そのようなプログラムを作成せよ。
方法
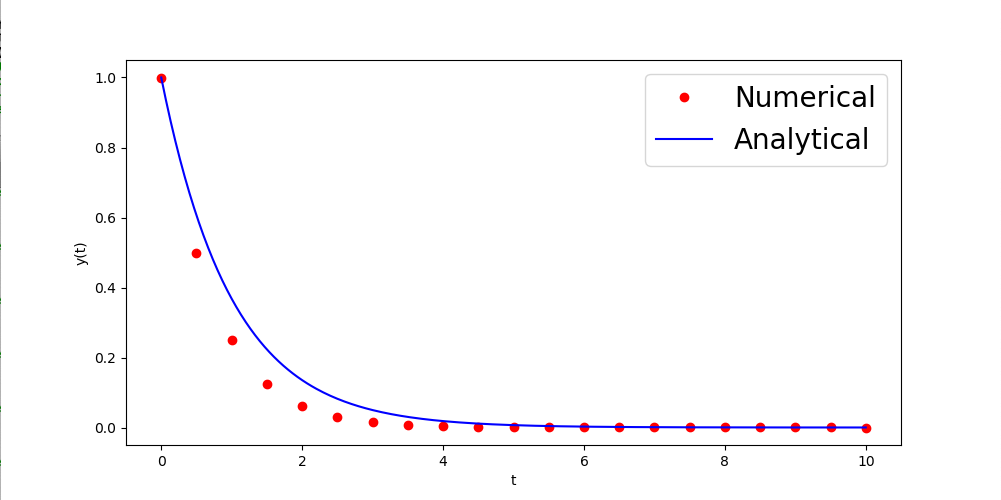
$N(t)$の値を(S )を用いて飛び飛びの$t$の値$t_i \ \ = \ \ dt * i$ （ただし$dt$は時間刻み幅）について求めるのであるが、(S )と課題６のグラフから明らかなように$N(t)$は単調減少関数である。であるから、$N(t_i) \ \ \geq 0.5N_0 \geq N(t_{i+1})$となる$i$があるであろう。このとき、 $t_i$を$\tau$の近似値$\tau^*$とする。$0 \ \ \leq t \ \ \leq 10$を100等分して上記方法にて$\tau$の近似値$\tau^*$を求め、課題8で求めた値との差（誤差と呼ぶ）$$err^* \ \ = \ \ | \tau-\tau^* | $$を求めよ。
注意：当然ながら刻み数を100から1000に増やせばより正確な値が求まる。
※参考：N (t )が具体的に与えられていない場合 （例えば実測データなど）にも有効なので、実用的です。
課題10 課題9の方法ではあまり良い精度で近似値を求めることができない。 次の方法でより精度良く近似値をもとめることを考える。
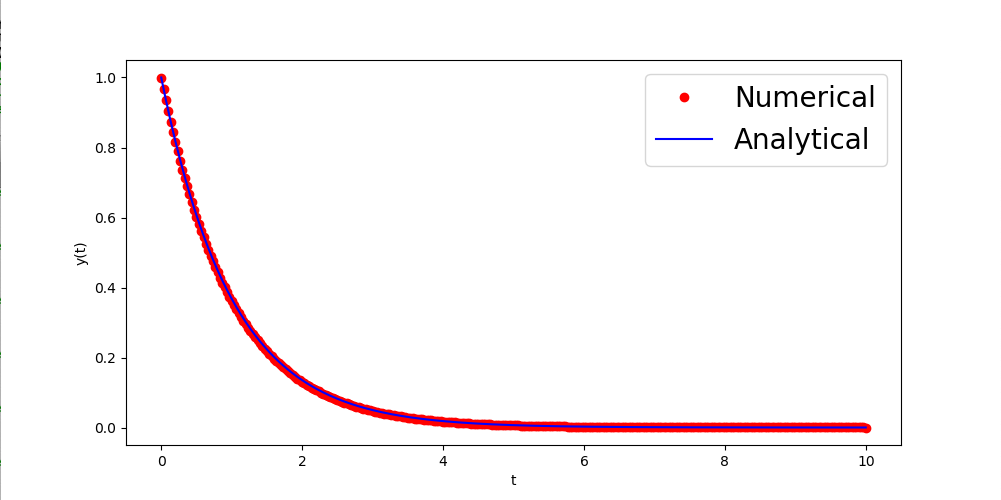
$N(t_i) \ \ \geq 0.5N_0 \geq N(t_{i+1})$となる$i$を求め、２点$(t_i, N(t_i)), \ \ (t_{i+1}, N(t_{i+1}))$ を結ぶ直線を考える。 その直線と$N=0.5$の直線の交点の$t$の値$\tau^{**}$をもって、$\tau$の近似値とする。 （このような手法を線形補間と呼ぶ。）$0 \ \ \leq t \leq 10$を100等分して上記方法にて$\tau$の近似値$\tau^{**}$を求め課題8で求めた値との差$$err^{**} \ \ = \ \ | \tau – \tau^{**} |$$
を求めよ。課題9の結果よりも良いだろうか？
注意： 課題9の方法でも刻み数を増やせばより正確な値が求まるのであるが、課題10の補間を使えば、あまり多くない刻み数でも正確な近似値が得られることを実感してほしい。
課題11 課題10において刻み数100で近似値を求めた場合の誤差と同程度に小さい誤差とするためには課題9において刻み数をどの程度にしなければならないか。実験してみよ。
課題12（余力のある人はトライ！） 課題9および課題10の方法において、横軸刻み数・縦軸err（半減期の真の解と数値解との誤差の絶対値）とした図を描け。
付録：matplotlibのanimation関数を使ったアニメーションの描画
方法1：全ての図を変数に格納し、パラパラ漫画的に描画
次は一度描かれたグラフのデータを変更するのではなく、少しずつずらしたグラフを用意して、そのたくさんのグラフを一つの関数に渡すことでまさに「パラパラ漫画」の要領でアニメーションを作る方法です。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig = plt.figure()
ax = fig.add_subplot(111)
x = np.arange(0, 10, 0.1)
y = np.sin(x)
dt = 0.05
v = 1.0
ims = []
for i in range(50):
t = dt * i
y = np.sin(x - v*t)
im = ax.plot(x, y, "r")
ims.append(im)
ani = animation.ArtistAnimation(fig, ims)
plt.show()
演習で行なったやり方（以下、方法0と呼びます）では、ax.plot関数はfor文の外側で一度使っただけですが、今回はfor文の中で毎回呼び出します。そして、そのグラフに関する情報をimとして受け取ります。方法0ではlinesを作るときにlinesの後ろに”, “がついていたのですが、今回はimの後ろに”, “がついていないことに注意してください。 そして、for文の直前に書いてあるims = []というコードは、そのパラパラ漫画を格納するためのリストですが、最初は空のリストです。ims.append(im)によって実際に格納していき、for文が終了するとimsの中に50枚の絵が用意されたと思ってください。 最後に用意されたimsとアニメーションを書き出したいキャンバスであるfigを引数として持つanimation.ArtistAnimation関数に二つの変数を渡すことでアニメーションを作ることが出来ます。
方法2：変化を定義する関数を与える方法
方法1にかなり近いやり方ですが、少し違う方法を紹介します。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig = plt.figure()
ax = fig.add_subplot(111)
x = np.arange(0, 10, 0.1)
y = np.sin(x)
dt = 0.05
v = 1.0
line, = ax.plot(x, y)
def init(): # only required for blitting to give a clean slate.
line.set_ydata([np.nan] * len(x))
return line,
def animate(i):
line.set_ydata(np.sin(x + i / 100))
# update the data.
return line,
ani = animation.FuncAnimation(fig, animate, init_func = init, frames=range(0,2*314,1), interval=1, blit=True, save_count=100)
plt.show()
この方法ではfor文を直接使わずに、animation.FuncAnimation関数にfor文で使われるコードをanimate関数として与えることでアニメーションを描いています。init_func関数で初期化し，animate関数でlineのy座標を更新・描画、framesがiに渡される引数でfor loop文の代わりの役目をしています．
どのやり方も一長一短なのですが、たぶん方法0が一番楽かと思います。 ただし、作ったアニメーションを動画形式で保存するには、方法1か方法2であると楽でしょう。
付録：Jupyter Notebookでアニメーションを見るための設定
※macOS Mojaveではこの方法は使えません！強制ログアウトされます！ macOS Catalinaでは解決しているようですが…
これまでグラフを描画してjupyter上で見るために、初めに
%matplotlib inline
と書いていました。アニメーションを見るためには、この方法では見られないため、以下のように変更してください。
%matplotlib tk
この部分を変更して実行しても、すでに先のコマンドを実行してjupyter notebookを使っている場合には、変更がききません。 新しく二つ目のコマンドを有効にするためには、いったんnotebookを閉じるか、ツールバーのkernelを選択してRestartをクリックして再起動する必要があります。
通りになります。それぞれの値の取り方によって、以下のような決まりによってRuleの番号が定められます。ちなみに藤井が個人的に好きなRuleは184です。（何故でしょう？）
が「（第一種不連続点のみをもつ）区分的に連続な周期
をもつ周期関数」であるとき、フーリエ級数は元の関数u(t)に各点収束します。
や
の先頭の 1/T の部分は 2/(積分区間) と考えると間違いが少ないです。
on ![[-1, 1]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-96395345c57f8928c42918c656dd1364_l3.svg)
の関数として拡張したものを考える。 この関数のフーリエ級数展開は、![\[ u(t) = \frac{1}{2} -\frac{4}{\pi^2}\sum_{n:odd} \frac{1}{n^2} \cos \pi n t \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-dcd303905760b42df566138c6efecfa0_l3.svg "Rendered by QuickLaTeX.com")
が奇数であること(つまり
について和をとること）を表している。 ここで、足し合わせる
として、![\[ u_N(t) = \frac{1}{2} -\frac{4}{\pi^2}\sum_{n:odd}^N \frac{1}{n^2} \cos \pi nt \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-2c5644db5b8f73b7fb70b1efae803162_l3.svg "Rendered by QuickLaTeX.com")
の場合における、
のグラフを図示せよ。
の範囲は
から
とせよ。 （
がそこそこまともに描画できる程度に、
![\[ d(t, N) = |u_N(t) - u(t) | \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-faeb47b1bc5351ddf3efb1efea4cf9f0_l3.svg "Rendered by QuickLaTeX.com")
における
の最大値を
とおき、
に収束するかどうか検証せよ。
は元の関数と
はもっともずれの大きい場所の![\[ u(t) = \left\{ \begin{array}{cc} 1 & (0 < t < \pi) \\ -1 & (-\pi < t < 0) \end{array} \right. \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-58fd72a30b82757fc5c8c75f418b4a88_l3.svg "Rendered by QuickLaTeX.com")
の関数として拡張したものを考え、不連続面(
)に注目する。
として、
のときのグラフ
![\[ d(t, N) = |u_N(t) - u(t)| \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-e2fd8fcd00d1f125ec051a3096a70787_l3.svg "Rendered by QuickLaTeX.com")
が
でどのように変化するかグラフで示せ。
と書けます。１次元拡散方程式（１次元熱伝導方程式とも呼ばれる）の初期値境界値問題を数値的に解きます。
および
）での拘束条件になります。
と
でいつも
となるディリクレ境界条件を境界に課しています。
のように離散化をしていたわけですが、もう一つ増えた空間を表す変数
についても同様に離散化をする必要があります。ただし、以下のように、空間方向の分割方法は時間方向の分割方法とは少し異なります。
等分した目盛り上に位置します。一方、空間方向の分割は、考える範囲を
を時間刻み幅としてきましたが、今後は
を時間刻み幅とします。すなわち、空間方向では![[0, L]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-400fcbb3cdc684be67816516e8d397d7_l3.svg)
区間を
）、時間方向では![[0, T]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-1b423ddb4cea2e2c7624a19269868604_l3.svg)
区間を
等分（
）して、
おくことができ、![\[ U^k_j \approx u(x_j, t_k), \ \ (j=1, \cdots, N, k= 0, 1, \cdots , M)\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-536212029b64ab246bc3b2f4ab5c9ae3_l3.svg "Rendered by QuickLaTeX.com")
![\[ \frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-0d6e0d58bc82ef095df3d2ae3b6b6fb3_l3.svg "Rendered by QuickLaTeX.com")
としました。
での
から次の時刻
での![\[u(0, t) = c,u(L, t) = c~(t>0)\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-9c876e85cd9e7975d26fbdf0361f63fc_l3.svg "Rendered by QuickLaTeX.com")
（今回は
）となるためには、境界の両隣の2点の中間値が![\[\displaystyle \frac{U_0^k+U_1^k}{2} = c\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-369ce02a945e4e2e8a3d199a464b8af6_l3.svg "Rendered by QuickLaTeX.com")
![\[U_0^k=2c-U_1^k~ (k=0, 1, 2, \cdots ,M)\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-4b1ce029a957788386f9211c15a99585_l3.svg "Rendered by QuickLaTeX.com")
![\[U_{N+1}^k = 2c-U_N^k~ (k=0, 1, 2, \cdots ,M) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-62d92bc5119a4e5b6991b824cc55551f_l3.svg "Rendered by QuickLaTeX.com")
![\[\frac{\partial u(0, t)}{\partial x} = 0, \frac{\partial u(L, t)}{\partial x} = 0~~(t>0)\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-fa0527427e9f90508d45a73dc9217ad8_l3.svg "Rendered by QuickLaTeX.com")
![\[\frac{\partial u(0, t)}{\partial x}\approx\frac{U_1^k-U_0^k}{h} = 0\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-1e7dad23e1fa578733b875f1ecba7613_l3.svg "Rendered by QuickLaTeX.com")
![\[U_0^k=U_1^k~ (k=0, 1, 2, \cdots ,M)\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-3bf4e7affde96f186b530d4ebef7c666_l3.svg "Rendered by QuickLaTeX.com")
![\[U_{N+1}^k = U_N^k~ (k=0, 1, 2, \cdots ,M) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-6e12ecb56ab3376a1e7bba546e53d083_l3.svg "Rendered by QuickLaTeX.com")
![\[u(x)=u(x+L)\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-112f58af8553ab54ce50960c7c9ee9e3_l3.svg "Rendered by QuickLaTeX.com")
や
とし、適当な自然数
とします。
とした）。
程度、
、境界条件はディリクレ条件とする。
としている。![\[ U_0^k = U_1^k, U_{N+1}^k = U_N^k \ \ (k=0, 1, 2, \cdots) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-cd7b62e42a5e1ba87cb3d23e003cc17f_l3.svg "Rendered by QuickLaTeX.com")
![\[ U_j^{k+1} = \alpha U_{j-1}^k + (1-2\alpha)U_j^k + \alpha U_{j+1}^k \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-737f6d1cb691b0fab70fabcaf21704fb_l3.svg "Rendered by QuickLaTeX.com")
での値から次の時刻
の値を直ちに計算できる形の差分方程式を陽公式(explicit scheme)と呼びます。陽公式を使った解法なので陽解法と呼びます。）
と三つの異なる場合について、同時にアニメーションに描画するpythonプログラムを作成し、Moodleから提出して下さい。
ならば
とした, 2(M+2) 個の連立微分方程式に対し, オイラー法（ルンゲ・クッタ法）を利用します.
をおもりの場所そのものとしても式(1)と同じ方程式になることと合わせて確認してみてください。
とする。
とする。）
を配列変数 Y1[j][m] で，
を配列変数 Y2[j][m] で表す.
は弦の変位をあらわします。
として、![\[ U_j^k \approx u(x_j, t_k) \ \ (j=1, \cdots, N, k=0, 1, \cdots) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-56d77de5c75af462d6328cd3b43121f3_l3.svg "Rendered by QuickLaTeX.com")
![\[ \frac{1}{\tau^2} (U_j^{k-1} - 2U_j^k + U_j^{k+1}) = \frac{c^2}{h^2} (U_{j-1}^{k} - 2U_j^k + U_{j+1}^{k})\ \ (j=1, \cdots, N, k=1, 2, \cdots) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-bdee4d82f10718589cdbc6ddf77271d5_l3.svg "Rendered by QuickLaTeX.com")
として、まとめると![\[U_j^{k+1} = 2U_j^k - U_j^{k-1} + \lambda^2(U_{j-1}^{k} - 2U_j^k + U_{j+1}^{k})\]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-5844c9b22e76ff076e151ac676dc75a6_l3.svg "Rendered by QuickLaTeX.com")
を計算するためには2つの時刻
及び
と
が必要となります。![\[ U_j^0 = f(x_i) \ \ (i=1, 2, \cdots, N) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-b6746235f73851ff8c6545cfa0c3344d_l3.svg "Rendered by QuickLaTeX.com")
はどのように決めれば良いでしょうか？![\[ u(x, \tau) = u(x, 0) + \tau\frac{\partial u(x, 0)}{\partial t} + \frac{\tau^2}{2} \frac{\partial^2 u(x, 0)}{\partial t^2} + O(\tau^3) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-c8599973ca1ecf3a4d78d39f793a95f4_l3.svg "Rendered by QuickLaTeX.com")
![\[ \frac{\partial u(x, 0)}{\partial t} = g(x) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-1868a15f4adce9a930e8a7ac6b9ea555_l3.svg "Rendered by QuickLaTeX.com")
![\[ \frac{\partial^2 u(x, 0)}{\partial t^2} = c^2 \frac{\partial^2 u(x, 0)}{\partial x^2} \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-f0e232ec5ddbf4f2917d992f580c4bcd_l3.svg "Rendered by QuickLaTeX.com")
![\[\frac{\partial^2 u(x, 0)}{\partial x^2} \approx \frac{c^2}{h^2} \{ u(x-h, 0) - 2u(x,0) + u(x+h, 0) \} \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-ecfc6600a3cfcb5cf02d51bbed92441f_l3.svg "Rendered by QuickLaTeX.com")
![\[ U_j^1 = U_j^0 + \tau g(x_j) + \frac{\lambda^2}{2} (U_{j-1}^0 - 2U_j^0 + U_{j+1}^0) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-5a09bc139f31f31be4259b8b28797d76_l3.svg "Rendered by QuickLaTeX.com")
![\[ U_0^k = - U_1^k, U_{N+1}^k = - U_N^k \ \ (k=1, 2, \cdots) \]](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-acb6e304eb37a607ea537a1c48bf0cf9_l3.svg "Rendered by QuickLaTeX.com")
が安定性のための必要十分条件です。
が上限でしたが、波動方程式では違う値になります。
となるように
を与えます。
程度、
で
程度) はそのままで、
および
を他のもにかえてみよ。例えば関数
、関数
のもと、進行波解
を実現するためには、どのようなパラメータで、どのような初期値から計算する必要が有るか。
程度となります。