コンテンツ
第9回
フーリエ級数
周期関数が「(第一種不連続点のみをもつ)区分的に連続な周期
をもつ周期関数」であるとき、フーリエ級数は元の関数u(t)に各点収束します。
よって、を
周期の関数とすると、
が成り立ちます。特にや
の先頭の 1/T の部分は 2/(積分区間) と考えると間違いが少ないです。
詳細は計算数理Aの講義で説明があると思いますので、ざっくりと概要だけ述べると、どんな周期関数も三角関数の線型結合で表現できて、各三角関数の重みがや
である、ということです。
無限級数をとったとき、フーリエ級数が元の関数に収束することは数学的に証明されています。
では、無限に足し合わせるのではなくて、有限個だけ足し合わせた場合は、どのような曲線が得られるでしょうか?
今回の演習では、足し合わせる項の数を増やして行ったときに、どのようにもとの関数に収束して行くのかをシミュレーションを通して見ていきましょう。
また、が不連続面を含む場合において、「滑らかな三角関数だけを足し合わせて、不連続な関数を近似する」という一見無茶なことをどのように実現しているのかを確認してみてください(課題3、4)。
課題1(ジグザグ波)
on
を周期の関数として拡張したものを考える。 この関数のフーリエ級数展開は、
となる。ただし、n:oddとはが奇数であること(つまり
について和をとること)を表している。 ここで、足し合わせる
の最大値を
として、
とおき、の場合における、
のグラフを図示せよ。
その際、のグラフも重ねて描画すること。 ただし、描画する
の範囲は
から
とせよ。 (
が大きいときについて:
がそこそこまともに描画できる程度に、
の刻み幅を小さくすることを意識してください)
小ネタ:関数の引数の参照渡しと値渡し
(少し難易度高めです。詳しいことは述べません。興味がある人は調べてみてください。)
関数にリスト(配列)を渡してまとめてできたらなぁ、と思う人がいるかもしれません。思わないし、別に興味ない、と言う人はこの小ネタは飛ばしてください。Pythonでは、関数の引数にリストを指定することも可能です。例えば、課題1において、以下の関数を定義すると便利かもしれません。
def a_n(n):
return -4/(np.pi*np.pi*n*n)
こうすれば、関数a_nにnが1, 3, 5, … , Nというリストの形で入ってきても、a_n(1), a_n(3), …, a_n(N)というリストの形で返ってきます(※ 「リスト * リスト」はリストの要素ごとの掛け算。内積ではない)。
では、についても同様に関数を定義しようと思います。
import numpy as np
import matplotlib.pyplot as plt
T=1
M=100
def u(tau):
for i in range(len(tau)):
while tau[i] > T:
tau[i] = tau[i] - 2*T
while tau[i] < -T:
tau[i] = tau[i] + 2*T
return np.abs(tau)
t = np.linspace(-2,2,M+1)
u_ans = u(t)
fig = plt.figure(figsize=(14,8))
ax = fig.add_subplot(111)
ax.plot(t, u_ans, "r-",label=r"ZigZag")
こうすれば、周期関数もうまく値が入ってくれそうです。ではこの状態で横軸をリストt、縦軸をu_ansでプロットすると、tがおかしなことになっていることがわかるとおもいます(下図)。
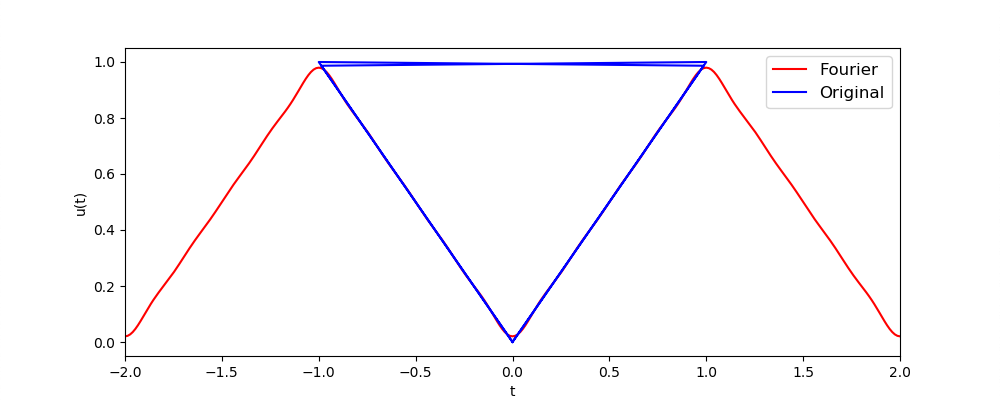
これは、Pythonでは、引数の受け渡しの実態は、値そのものではなく、値が格納されている場所(変数が参照している場所)を渡しているからです。これを参照渡しと呼びます。(対して、値そのものを受け渡していることを値渡しと呼びます。)そのため、関数の中で変数tau(仮引数)を変更すると、同時に関数の外の変数t(実引数)も変更していることになってしまっており、グラフ描画の際にtが元々の値から変わってしまったわけです。
ちなみに、Pythonでは引数を参照渡しで渡していますが、実変数を変更される型(mutable型、リスト・辞書型など)と変更されない型(immutable型、数値(スカラー)・文字列など)があります。immutable型の場合は、きちんと代わりの変数の場所が用意され、実引数は影響を受けません(そのため見かけ上は値渡しと同じように動作します)。
では、実際にリストを引数とするときに、実引数に影響を与えないようにするにはどうすれば良いのか、ですが、以下のようにcopyモジュールのdeepcopyを使います。
import numpy as np
import matplotlib.pyplot as plt
import copy
T=1
M=100
def u(tau):
tmp = copy.deepcopy(tau)
for i in range(len(tmp)):
while tmp[i] > T:
tmp[i] = tmp[i] - 2*T
while tmp[i] < -T:
tmp[i] = tmp[i] + 2*T
return np.abs(tmp)
t = np.linspace(-2,2,M+1)
u_ans = u(t)
fig = plt.figure(figsize=(14,8))
ax = fig.add_subplot(111)
ax.plot(t, u_ans, "r-",label=r"ZigZag")
こうすることで、実引数の値そのものを受け渡すことができます。単にtmp = tauとしてしまうと、また参照渡しになってしまうので、無意味になってしまいますのでご注意を。
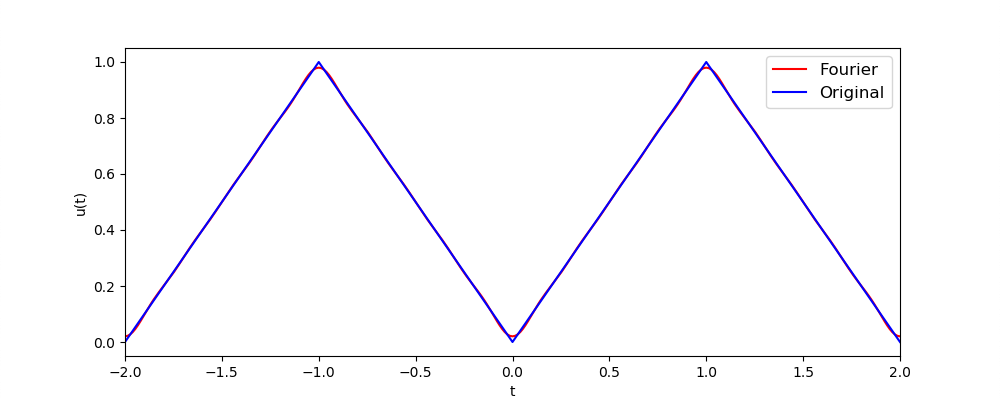
この辺りの話は、C言語でも配列を引数にする方法があるにはありますが、そのために「ポインタとアドレス」という概念を学ぶ必要があります(計算数学演習では扱いません)。このような概念を知っていると、他の言語への応用がきき、両方の言語のより深い理解に繋がります。
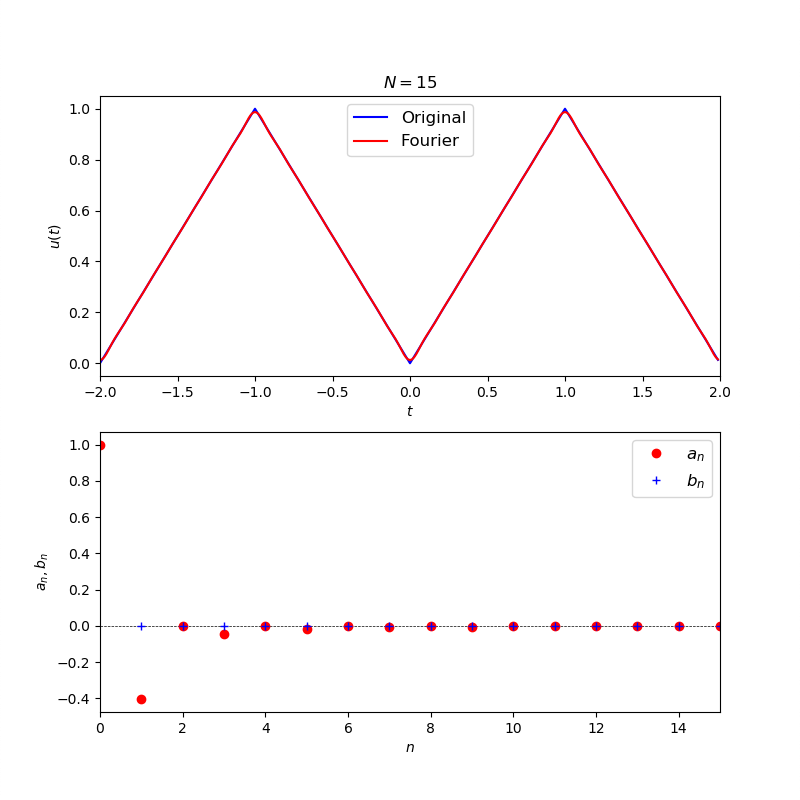
課題1′
課題1 では、すでに数値積分を解析的に解いた式をプロットしたが、すでに諸君は数値積分で近似的に求める方法を知っているはずである。そこで、関数u(t)さえ定義してしまえば、自動的におよび
が求まるような仕様に変更せよ。さらに、横軸を
とし、縦軸に
および
としたグラフも表示するプログラムを作成せよ。(課題1の場合、
は
によらずほぼ0になるはずである。)
課題2(ジグザグ波の続き)
とする。このとき、における
の最大値を
とおき、
を画面に表示できるように、課題1のプログラムを改良せよ。
を動かして、
が
に収束するかどうか検証せよ。
(は元の関数と
とののズレを表している。
はもっともずれの大きい場所の
の値に相当する。)
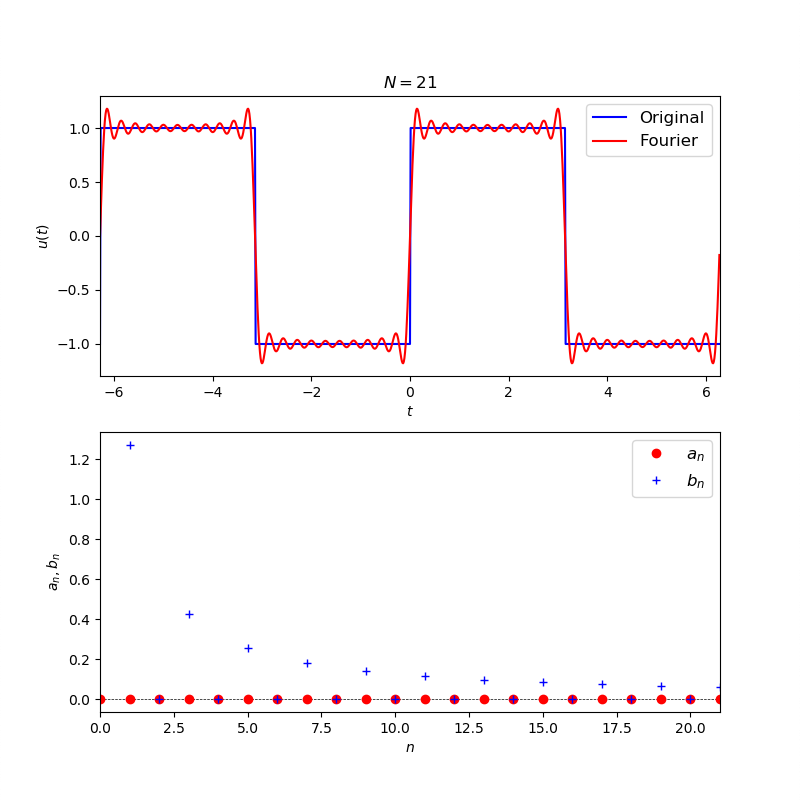
課題3 ギブス現象
次の式(矩形波)
を周期の関数として拡張したものを考え、不連続面(
)に注目する。
を有限の
に対してフーリエ級数展開した関数を
とし、
の値を変化させた場合において、不連続面近くのグラフを描画せよ。
ただし、描画する範囲を、として、
キーボードからの入力を促し、
と
を重ねて描画せよ。
参考:のときのグラフ
課題4
課題3の式について、不連続点以外のについて、
が
に収束するかどうかを確認するため、
とし、が
でどのように変化するかグラフで示せ。
