コンテンツ
第13回
波動方程式の数値解法
今回は1次元波動方程式(wave equation)を扱います。
ここでは、1次元波動方程式をコンピュータを用いて解くために差分化を行い、コンピュータを用いて波動方程式を解くアルゴ リズムを示します。
今日の内容に関する詳しい情報は講義で説明があります(ました)。
演習では細かい事は気にせずに一気にアルゴリズムの紹介まで行きたい と思います。
さ て、天下り的ですが1次元波動方程式は弦の振動をあらわします。
(導出等は講義で説明されます。また前回の「連結バネ系」からも導出できます。時間があれば紹介します。)
下記方程式 (W) におけるは弦の変位をあらわします。
演習では1次元波動方程式を数値計算を用いて解き、その解を画面上にアニメーションとして表示する事を目標とします。
つまり、コンピュータ内部に弦の振動を再現し、それをアニメーションとして表示するわけです。
時間-空間2階偏微分方程式の差分化
さて、次の1次元波動方程式の初期値境界値問題、
\[
\left\{
\begin{array}{l}
\frac{\partial ^2 u(x, t)}{\partial t^2} \ \ = \ \ c^2 \frac{\partial ^2 u(x, t)}{\partial x^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (0 < x <l, t >0)\\
u(0, t) \ \ = u(l, t) \ \ = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (t>0)\\
u(x, 0) \ \ = f(x), \ \ \ \ \frac{\partial u(x, 0)}{\partial t} \ \ = \ \ g(x) \ \ \ \ \ \ (0 < x <l)\\
\end{array}
\right. \ \ \ \ \ \ \ \ (W)
\]
但し、$c>0, f(0)=0, f(L)=0, g(0)=0, g(L)=0$を考えます。
境界条件、初期条件が適切に与えられれば式(W)の解が弦の振動を表現していると言えるでしょう。
さて、数値計算する為にまず式(W)を離散化する必要があります。
これまでの演習で拡散方程式の数値解法を扱いましたが、そこでは時間方向の離散化として下図の(1)を、空間方向の離散化として下図の(2)を採用してきました。今回も同様です。
区間を
等分するとし、上記離散化方法に従い、$h=L/N, \tau>0$とし、
として、
と書くことにすると、(W)の第一式は次のように離散化されます。
として、まとめると
という漸化式が得られます。
2階微分の差分化については、このページ最後のスライドを参照してください。
初期条件
初期条件も差分化する必要がありますが、拡散方程式のときと異なる点があります。
先ほどの離散化した漸化式において、次の時刻での
を計算するためには2つの時刻
及び
での
が必要です。
したがって、漸化式を順次計算する上で、まずはと
が必要となります。
まずは(W)の第三式より、
となることは良いでしょう。でははどのように決めれば良いでしょうか?
を決める方法はいくつか考えられますが、例えば次のようにします。
まず、テイラーの公式を用いると、
となります。ここで式(W)のまだ使っていない条件
を使います。さらにでも(W)の第一式が成り立つとすると、
となります。この式の右辺は2階差分商を用いて
と近似できます。つまり、
と求まります。
境界条件
境界条件については拡散方程式のときと同様です。今回の(W)における境界条件は Dirichlet条件ですので、
となります。
他の境界条件の場合については、第10回を参考にして下さい。
解くべき(差分)方程式
以上の考察から解くべき式をまとめると、以下のようになります。
\[
\left\{
\begin{array}{l}
U_j^{k+1} \ \ = \ \ 2U_j^{k} – U_j^{k-1}+ \lambda^2(U_{j-1}^k-2U_j^k + U_{j+1}^k)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (j=1 \cdots, N, \ \ k=1,2,)\\
\frac{U_0^k+U_1^k}{2}=0, \ \ \frac{U_N^k+U_{N+1}^k}{2}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (k=1,2,\cdots)\\
U_j^0 \ \ = \ \ f(x_j) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (j=1,\cdots, N) \\
U_j^1 \ \ = \ \ U_j^0 + \tau g(x_j) + \frac{ \lambda^2}{2}(U_{j-1}^0 -2U_j^0+ U_{j+1}^0) \\
\end{array}
\right. \ \ \ \ \ \ \ \ (2)
\]
ただし、が安定性のための必要十分条件です。
拡散方程式ではが上限でしたが、波動方程式では違う値になります。
(安定性条件とは、数値計算がうまく行く為の条件ですなぜにこういった条件が必要であるかは、講義で説明があります)。
めでたく差分方程式が得られました。
(2)をコンピューターを用いて解くのが目標です。
アルゴリズム
あくまで、参考用です。始めに自分で解き方を考えてください。
1次元波動方程式を解く為のアルゴリズムは次のようになります。
安定性条件を満たすためとなるように
を与えます。
空間用の箱が何個必要なのかについては,第10回講義の拡散方程式の実装で紹介した
ルーチン図を参考に考えてください.
(1)初期パラメータ設定T(時間上限), N(時間刻み数), L(空間幅), M(空間刻み数), c を設定する
τ=T/N, h = L/M, λ = τ*c/h (λ ≦ 1 となるように. M, N を調整, プログラム中では, λは「lamb」, τは「tau」などとするとよい.)
(2) 初期値設定
#必要な箱の準備
t_vec = #時間用1次元ベクトル
X_vec = #空間用1次元ベクトル
U= #二次元配列(時間ID, 空間ID)
#初期値代入
U[0]= #f(xi)の式
#境界条件:dilekli
U[0][0]= ???など
U[1]= #テイラー展開から考えた式(ちなみにg(x) は課題1,2を参照)
#境界条件:dilekli
U[1][0]= ???など
(3) 更新計算
k := 1,.....,N の順に
j := 1,.....,M の順に
??? = ???? #更新式を書く
(境界条件:dilekli)
u[k][0] = -u[k][1], u[k][M+1] = -u[k][M]
(4)動画描画
#グラフの準備
(x[k][0], u[k][0], x[k][M+1], u[k][M+1] は境界処理用なので表示しない)
k := 0,....,N の順に
(iii)描画 一定間隔毎に(例えば (j+1)%100==0 の時に, 等)
(x[1], u[1]) ~ (x[N], u[N]) を画面に表示 #(x[k][0], u[k][0], x[k][M+1], u[k][M+1] は境界処理用なので表示しない)
を繰り返す
課題1
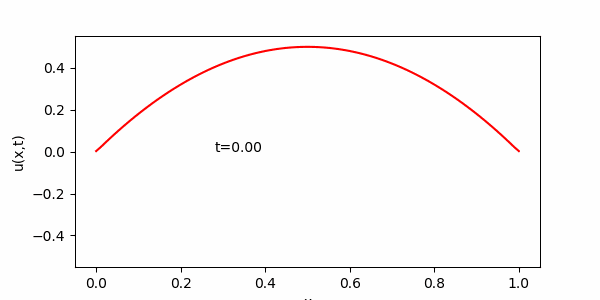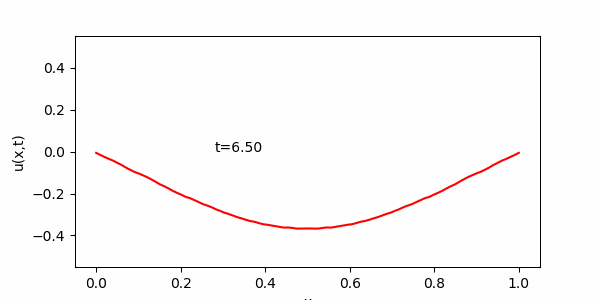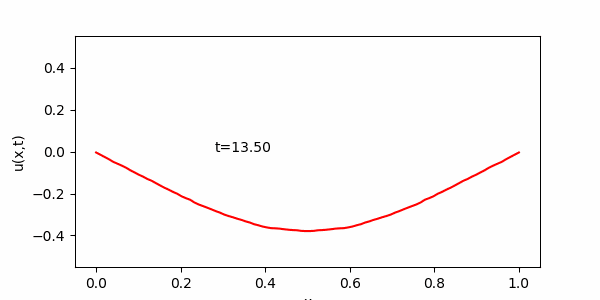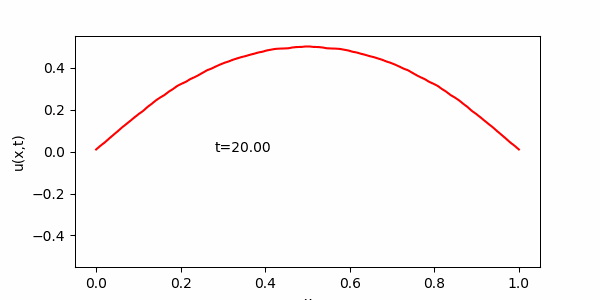
$L=1, c=0.1,\ \ f(x)=2x(1-x),\ \ g(x)=0,\ \ u(0,t)=\ u(1,t) =\ 0$として (2) を解くプログラムを作成せよ。
(は
程度、
で
となるように
を適度に選び, 描写頻度も適度に選ぶ事。)
課題2
$L=1, c=0.1,\ \ u(0,t)=\ u(1,t) =\ 0$(程度) はそのままで、
および
を他のもにかえてみよ。例えば関数
、関数
を
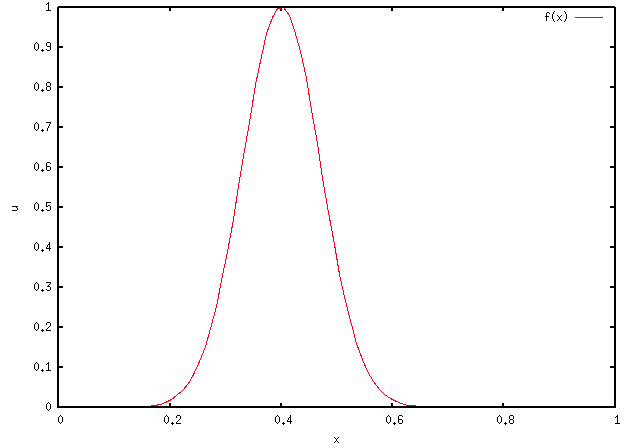
としたり
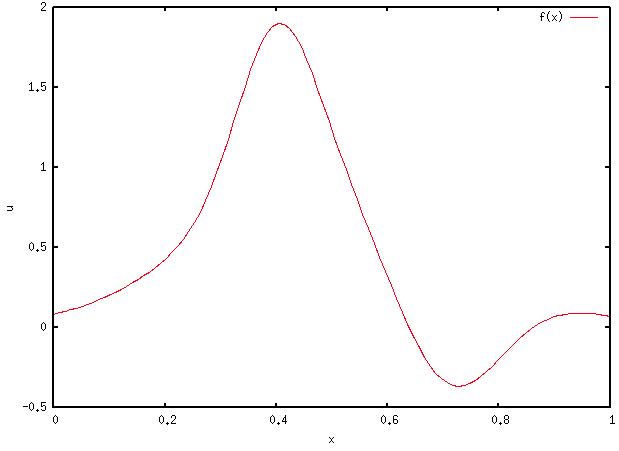
とする等。
(局在化した初期値からはじめると、波の伝播が観察される。)
課題3
境界条件を、Neumann境界条件や周期境界条件を適応したプログラムを作成し、実際に数値計算してみよ。
周期境界条件のもと、進行波解
を実現するためには、どのようなパラメータで、どのような初期値から計算する必要が有るか。
発展課題1
弦の振動ではなく、膜の振動を考えたい。すなわち、1次元波動方程式ではなく2次元波動方程式を考える。どのような方程式になるであろうか?
発展課題2
2次元波動方程式を差分化し、プログラムを作成し、数値計算せよ。
Pythonでの3次元プロットの方法は各自調べてみてください。
補足:差分近似について



導関数の差分近似について
関数 u(x) を x のまわりでTaylor展開すると
(S1)
(S2)
となり、両辺を加えると、
(S3)
となります。O(d4)を無視すると、
(S4)
この式の右辺の誤差は程度となります。
展開すると
(S1)
(S2)
となり、両辺を加えると、
(S3)
となります。O(d4)を無視すると、
(S4)
この式の右辺の誤差は程度となります。
